题目内容
如图:已知四面体PABC的所有棱长均为3cm,E、F分别是棱PC,PA上的点,且
PF=FA,PE=2EC,则棱锥B-ACEF的体积为______.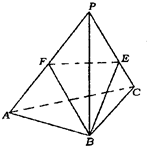
PF=FA,PE=2EC,则棱锥B-ACEF的体积为______.

当棱长为3时
正四面体的底面积S=
×32=
正四面体的高h=
•3=
故正四面体的体积V=
•S•h=
×
×
=
而SACEF:S△PAC=1-
=2:3
所以锥B-ACEF的体积为
×
=
cm3
故答案为:
cm3
正四面体的底面积S=
| ||
| 4 |
9
| ||
| 4 |
正四面体的高h=
| ||
| 3 |
| 6 |
故正四面体的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
9
| ||
| 4 |
| 6 |
9
| ||
| 4 |
而SACEF:S△PAC=1-
| PE•PF |
| PC•PA |
所以锥B-ACEF的体积为
| 2 |
| 3 |
9
| ||
| 4 |
3
| ||
| 2 |
故答案为:
3
| ||
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知四面体P-ABC中,PA=PB=PC,且AB=AC,∠BAC=90°,则异面直线PA与BC所成的角为
如图,已知四面体P-ABC中,PA=PB=PC,且AB=AC,∠BAC=90°,则异面直线PA与BC所成的角为 (2011•焦作一模)如图:已知四面体PABC的所有棱长均为3cm,E、F分别是棱PC,PA上的点,且
(2011•焦作一模)如图:已知四面体PABC的所有棱长均为3cm,E、F分别是棱PC,PA上的点,且