题目内容
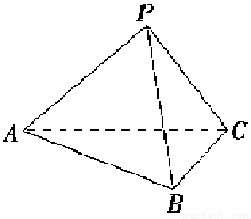
如图：已知四面体PABC的所有棱长均为3cm，E、F分别是棱PC，PA上的点，且PF=FA，PE=2EC，则棱锥B-ACEF的体积为 ．
【答案】分析：由已知中正四面体的所有棱长都为3，可分别求出棱锥的底面面积和高，代入棱锥体积公式，即可得到答案．
解答：解：当棱长为3时
正四面体的底面积S=
=
正四面体的高h=
•3=
故正四面体的体积V=
•S•h=
=
而SACEF：S△PAC=1-
=2：3
所以锥B-ACEF的体积为
=
故答案为：
点评：本题考查的知识点是棱锥的体积公式，由于正四面体在考试中比较容易考查，故熟练掌握棱长为a的正四面体的底面积、高、体积、表面积、内切球半径、外切球半径…的公式，是提高解答正四面体问题速度和精度的关键．
解答：解：当棱长为3时
正四面体的底面积S=
=正四面体的高h=
•3=故正四面体的体积V=
•S•h==而SACEF：S△PAC=1-
=2：3所以锥B-ACEF的体积为
=故答案为：
点评：本题考查的知识点是棱锥的体积公式，由于正四面体在考试中比较容易考查，故熟练掌握棱长为a的正四面体的底面积、高、体积、表面积、内切球半径、外切球半径…的公式，是提高解答正四面体问题速度和精度的关键．
练习册系列答案
相关题目
如图，已知四面体P-ABC中，PA=PB=PC，且AB=AC，∠BAC=90°，则异面直线PA与BC所成的角为
（2011•焦作一模）如图：已知四面体PABC的所有棱长均为3cm，E、F分别是棱PC，PA上的点，且
