题目内容
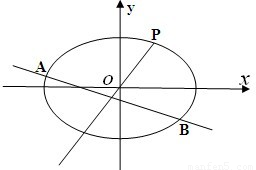
 (1)如图,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点,如果A,B两点的纵坐标分别为
(1)如图,在平面直角坐标系中,锐角α和钝角β的终边分别与单位圆交于A,B两点,如果A,B两点的纵坐标分别为| 3 |
| 5 |
| 12 |
| 13 |
(2)已知cos(
| π |
| 2 |
| ||
| 2 |
| π |
| 2 |
分析:(1)直接由三角函数的定义写出sinα,sinβ的值,由同角三角函数的基本关系式求解cosβ的值;
(2)由已知求出sinφ,结合φ的范围求出φ的值,则tanφ的值可求.
(2)由已知求出sinφ,结合φ的范围求出φ的值,则tanφ的值可求.
解答:解:(1)根据三角函数的定义,得sinα=
,sinβ=
,
又β是钝角,∴cosβ=-
=-
=-
;
(2)∵cos(
+φ)=-sinφ=
,
∴sinφ=-
.
∵|φ|<
,∴φ=-
,
∴tanφ=tan(-
)=-tan
=-
.
| 3 |
| 5 |
| 12 |
| 13 |
又β是钝角,∴cosβ=-
| 1-sin2β |
1-(
|
| 5 |
| 13 |
(2)∵cos(
| π |
| 2 |
| ||
| 2 |
∴sinφ=-
| ||
| 2 |
∵|φ|<
| π |
| 2 |
| π |
| 3 |
∴tanφ=tan(-
| π |
| 3 |
| π |
| 3 |
| 3 |
点评:本题考查了任意角的三角函数的定义,考查了同角三角函数的基本关系式,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).(已知在通道的分叉处,小弹子以相同的概率落入每个通道) 如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).(已知在通道的分叉处,小弹子以相同的概率落入每个通道)
如图是在竖直平面内的一个“通道游戏”.图中竖直线段和斜线段都表示通道,并且在交点处相遇,若竖直线段有第一条的为第一层,有二条的为第二层,…,依此类推.现有一颗小弹子从第一层的通道里向下运动.记小弹子落入第n层第m个竖直通道(从左至右)的概率为P(n,m).(已知在通道的分叉处,小弹子以相同的概率落入每个通道) 如图,在平面直坐标系xOy中,已知椭圆
如图,在平面直坐标系xOy中,已知椭圆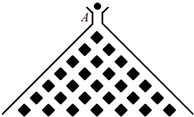 (2011•丹东模拟)如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑滑道,黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
(2011•丹东模拟)如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑滑道,黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是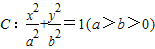 ,经过点(1,e),其中e为椭圆的离心率.且椭圆C与直线
,经过点(1,e),其中e为椭圆的离心率.且椭圆C与直线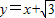 有且只有一个交点.
有且只有一个交点.