题目内容
（2013•嘉兴一模）若
，
是两个非零向量，且|
|=|
|=λ|
+
|，λ∈[
，1]，则
与
-
的夹角的取值范围是
| a |
| b |
| a |
| b |
| a |
| b |
| ||
| 3 |
| b |
| a |
| b |
[
，
）
| π |
| 3 |
| 5π |
| 6 |
[
，
）
．| π |
| 3 |
| 5π |
| 6 |
分析：不妨设|
+
|=1，则|
|=|
|=λ．令
=
，
=
，以OA、OB为临边作平行四边形OACB，则平行四边形OACB
为菱形．故有∠OAB=∠OBA=θ，
与
-
的夹角，即
与
的夹角，等于π-θ，且0＜θ＜
．△OAC中，由
余弦定理解得 cos2θ=1-
．再由
≤λ≤1求得cos2θ的范围，从而求得θ的范围，即可得到
与
-
的
夹角的取值范围．
| a |
| b |
| a |
| b |
| OA |
| a |
| OB |
| b |
为菱形．故有∠OAB=∠OBA=θ，
| b |
| a |
| b |
| OB |
| BA |
| π |
| 2 |
余弦定理解得 cos2θ=1-
| 1 |
| 2λ2 |
| ||
| 3 |
| b |
| a |
| b |
夹角的取值范围．
解答：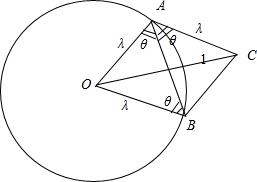
解：∵|
|=|
|=λ|
+
|，λ∈[
，1]，
不妨设|
+
|=1，则|
|=|
|=λ．
令
=
，
=
，以OA、OB为邻边作平行四边形OACB，
则平行四边形OACB为菱形．
故有△OAB为等腰三角形，故有∠OAB=∠OBA=θ，
且0＜θ＜
．
而由题意可得，
与
-
的夹角，即
与
的夹角，
等于π-θ．
△OAC中，由余弦定理可得 OC2=1=OA2+AC2-2OA•AC•cos2θ=λ2+λ2-2•λ•λcos2θ，
解得 cos2θ=1-
．
再由
≤λ≤1，可得
≤
≤
，∴-
≤cos2θ≤
，∴
＜2θ≤
，∴
＜θ≤
，
故
≤π-θ＜
，即
与
-
的夹角π-θ的取值范围是[
，
）．
解：∵|| a |
| b |
| a |
| b |
| ||
| 3 |
不妨设|
| a |
| b |
| a |
| b |
令
| OA |
| a |
| OB |
| b |
则平行四边形OACB为菱形．
故有△OAB为等腰三角形，故有∠OAB=∠OBA=θ，
且0＜θ＜
| π |
| 2 |
而由题意可得，
| b |
| a |
| b |
| OB |
| BA |
等于π-θ．
△OAC中，由余弦定理可得 OC2=1=OA2+AC2-2OA•AC•cos2θ=λ2+λ2-2•λ•λcos2θ，
解得 cos2θ=1-
| 1 |
| 2λ2 |
再由
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 2λ2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 3 |
故
| π |
| 3 |
| 5π |
| 6 |
| b |
| a |
| b |
| π |
| 3 |
| 5π |
| 6 |
点评：本题主要考查两个向量的加减法及其几何意义，余弦定理以及不等式的性质的应用，属于中档题．
练习册系列答案
相关题目
（2013•嘉兴一模）如图，直角梯形ABCD中，AB∥CD，∠BCD=90°，BC=CD=
（2013•嘉兴一模）一个几何体的三视图如图所示，则该几何体的体积为