题目内容
函数y=
的定义域为[0，
]，则函数的值域为（ ）
| sinx-3 |
| cosx-2 |
| π |
| 2 |
A、[
| ||||||||
| B、[1，3] | ||||||||
C、[
| ||||||||
D、[2-
|
分析：本题给出的表达式y=
，恰好符合已知两点（x1，y1），（x2，y2）求斜率的公式：k=
，故利用图象法求解．
| sinx-3 |
| cosx-2 |
| y2-y1 |
| x2-x′ |
解答：
解：数形结合法：y=
的可看作：
点（2，3）与圆x2+y2=1上的点（cosx，sinx）x∈[0，
]的连线的斜率的范围
如图，圆上的点只取第一象限内的部分．
由图可知，当圆上的点处在B处时，直线AB的斜率最大，为3；
当圆上的点处在C时，直线AC斜率最小，为1；
则函数的值域为[1，3]．
故选B．
解：数形结合法：y=| sinx-3 |
| cosx-2 |
点（2，3）与圆x2+y2=1上的点（cosx，sinx）x∈[0，
| π |
| 2 |
如图，圆上的点只取第一象限内的部分．
由图可知，当圆上的点处在B处时，直线AB的斜率最大，为3；
当圆上的点处在C时，直线AC斜率最小，为1；
则函数的值域为[1，3]．
故选B．
点评：若已知A（x1，y1），B（x2，y2），则AB所在直线的斜率 k=
，数形结合思想有时候解决问题很有效．
| y2- y1 |
| x2 -x1 |
练习册系列答案
相关题目
把函数y=sinx的图象上所有点向右平移
个单位，再将图象上所有点的横坐标缩小到原来的
（纵坐标不变），所得解析式为y=sin（ωx+φ），则（ ）
| π |
| 3 |
| 1 |
| 2 |
A、ω=2，φ=
| ||||
B、ω=2，φ=-
| ||||
C、ω=
| ||||
D、ω=
|
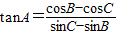成立，则△ABC为A=60°的三角形．