题目内容
已知向量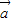 =(cosθ,sinθ),θ∈[0,π],向量
=(cosθ,sinθ),θ∈[0,π],向量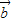 =(
=(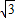 ,-1)
,-1)(1)当
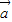 ∥
∥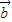 ,求θ.
,求θ.(2)当
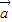 ⊥
⊥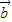 时,求θ
时,求θ
【答案】分析:(1)由向量共线的坐标表示得三角等式,求出角θ的正切值后根据角的范围可得答案;
(2)由向量垂直的坐标表示得三角等式,求出角θ的正切值后根据角的范围可得答案
解答:解:由向量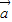 =(cosθ,sinθ),向量
=(cosθ,sinθ),向量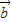 =(
=(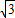 ,-1)
,-1)
(1)若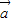 ∥
∥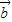 ,则
,则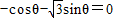 ,即
,即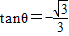 ,
,
因为θ∈[0,π],所以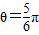 ;
;
(2)若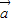 ⊥
⊥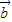 ,则
,则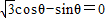 ,即
,即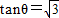 .
.
因为θ∈[0,π],所以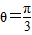 .
.
点评:本题考查了向量平行及垂直的坐标表示,考查了由三角函数值求角,是基础题.
(2)由向量垂直的坐标表示得三角等式,求出角θ的正切值后根据角的范围可得答案
解答:解:由向量
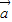 =(cosθ,sinθ),向量
=(cosθ,sinθ),向量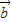 =(
=(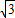 ,-1)
,-1)(1)若
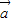 ∥
∥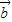 ,则
,则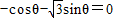 ,即
,即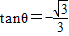 ,
,因为θ∈[0,π],所以
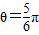 ;
;(2)若
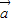 ⊥
⊥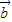 ,则
,则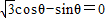 ,即
,即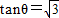 .
.因为θ∈[0,π],所以
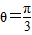 .
.点评:本题考查了向量平行及垂直的坐标表示,考查了由三角函数值求角,是基础题.

练习册系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |