题目内容
在长方体ABCD-A1B1C1D1中,AB=AD=2,AA1=a,E,F分别为AD,CD的中点.
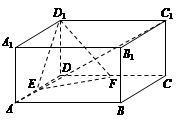
(1)若AC1⊥D1F,求a的值;
(2)若a=2,求二面角E-FD1-D的余弦值.
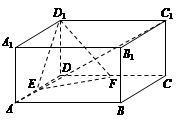
(1)若AC1⊥D1F,求a的值;
(2)若a=2,求二面角E-FD1-D的余弦值.
(1)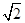 ;(2)
;(2)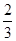
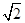 ;(2)
;(2)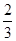
试题分析:(1)首先建立空间直角坐标系,列出各对应点坐标,表示对应向量坐标,
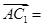 (-2,2,a),
(-2,2,a),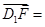 (0,1,-a),再根据空间向量数量积定义,得到2-a2=0,从而求出a的值,(2)先判断二面角E-FD1-D为锐二面角,所以求二面角E-FD1-D的余弦值,就转化为求两个平面法向量夹角的余弦值的绝对值.又平面FD1D的一个法向量为
(0,1,-a),再根据空间向量数量积定义,得到2-a2=0,从而求出a的值,(2)先判断二面角E-FD1-D为锐二面角,所以求二面角E-FD1-D的余弦值,就转化为求两个平面法向量夹角的余弦值的绝对值.又平面FD1D的一个法向量为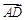 ,所以关键求平面EFD1的一个法向量n=(x,y,z),利用 n⊥
,所以关键求平面EFD1的一个法向量n=(x,y,z),利用 n⊥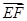 ,n⊥
,n⊥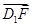 可求出x=y=2z,取其一个法向量为n=(2,2,1),再利用空间向量夹角公式
可求出x=y=2z,取其一个法向量为n=(2,2,1),再利用空间向量夹角公式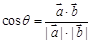 ,就可得到二面角E-FD1-D的余弦值.
,就可得到二面角E-FD1-D的余弦值.试题解析:解 如图,以D为坐标原点,DA所在直线为x轴,
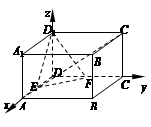
DC所在直线为y轴,DD1所在直线为z轴,建立坐标系.
(1)由题意得A(2,0,0),D1(0,0,a),C1(0,2,a),F(0,1,0).
故
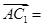 (-2,2,a),
(-2,2,a),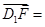 (0,1,-a). 2分
(0,1,-a). 2分因为AC1⊥D1F,所以
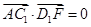 ,即(-2,2,a)·(0,1,-a)=0.
,即(-2,2,a)·(0,1,-a)=0.从而2-a2=0,又a>0,故
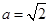 . 5分
. 5分(2)平面FD1D的一个法向量为m=(1,0,0). 设平面EFD1的一个法向量为n=(x,y,z),
因为E(1,0,0),a=2,故
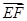 =(-1,1,0),
=(-1,1,0),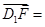 (0,1,-2).
(0,1,-2).由n⊥
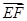 ,n⊥
,n⊥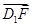 ,得-x+y=0且y-2z=0,解得x=y=2z.
,得-x+y=0且y-2z=0,解得x=y=2z.故平面EFD1的一个法向量为n=(2,2,1). 8分
因为
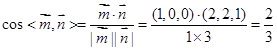 ,且二面角E-FD1-D的大小为锐角,
,且二面角E-FD1-D的大小为锐角,所以二面角E-FD1-D的余弦值为
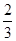 . 10分
. 10分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,侧棱
中,侧棱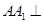 平面
平面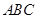 ,
,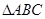 为等腰直角三角形,
为等腰直角三角形,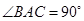 ,且
,且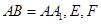 分别是
分别是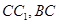 的中点.
的中点.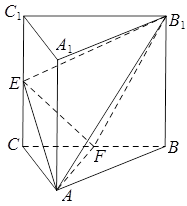
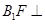 平面
平面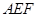 ;
;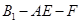 的余弦值.
的余弦值.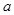 .
.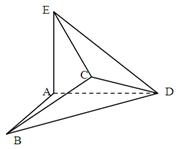
 ,求证:AB∥平面CDE;
,求证:AB∥平面CDE;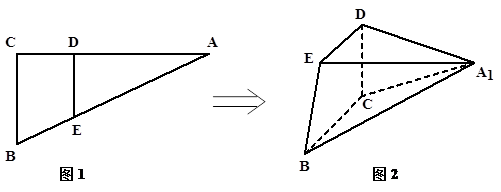
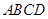 的顶点
的顶点 分别在两两垂直的三条射线
分别在两两垂直的三条射线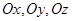 上,则在下列命题中,错误的为( )
上,则在下列命题中,错误的为( )
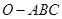 是正三棱锥
是正三棱锥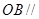 平面
平面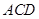
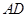 与
与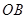 所成的角是
所成的角是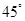
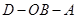 为
为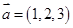 ,
,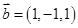 构成的向量集合
构成的向量集合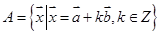 ,则向量
,则向量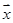 的模
的模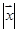 的最小值为 .
的最小值为 .