题目内容
设A、B、C及A1、B1、C1分别是异面直线l1、l2上的三点,而M、N、P、Q分别是线段AA1、BA1、BB1、CC1的中点.求证:M、N、P、Q四点共面
证明: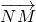 =
=
 ,
,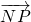 =
=
 ,
,
∴ =2
=2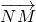 ,
, =2
=2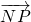 .
.
又∵ =
= (
( +
+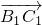 ),(*)
),(*)
A、B、C及A1、B1、C1分别共线,
∴ =λ
=λ =2λ
=2λ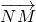 ,
,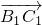 =ω
=ω =2ω
=2ω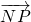 .
.
代入(*)式得 =
= (2λ
(2λ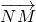 +2ω
+2ω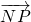 )=λ
)=λ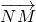 +ω
+ω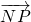 ,∴
,∴ 、
、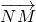 、
、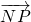 共面.
共面.
∴M、N、P、Q四点共面.
分析:根据题中的连线情况可知:MN、NP这两条线段分别可以放到△AA1B、△BA1B1中,利用中位线定理找出它们的大小及平行关系,进行转化,而PQ则比较麻烦,没有一个现成的平面可以将其放进去,如果想把PQ转化成BC及B1C1的话,可以联想到向量进行转化,然后再由A、B、C及A1、B1、C1分别共线,设定比例,再代入解决.
点评:此题将平面向量的基本定理运用到立体几何中的四点共面问题,是个不错的方法,体现了知识之间的相互联系.
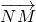 =
=
 ,
,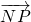 =
=
 ,
,∴
 =2
=2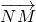 ,
, =2
=2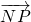 .
.又∵
 =
= (
( +
+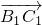 ),(*)
),(*)A、B、C及A1、B1、C1分别共线,
∴
 =λ
=λ =2λ
=2λ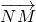 ,
,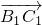 =ω
=ω =2ω
=2ω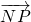 .
.代入(*)式得
 =
= (2λ
(2λ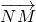 +2ω
+2ω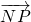 )=λ
)=λ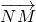 +ω
+ω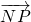 ,∴
,∴ 、
、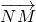 、
、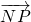 共面.
共面.∴M、N、P、Q四点共面.
分析:根据题中的连线情况可知:MN、NP这两条线段分别可以放到△AA1B、△BA1B1中,利用中位线定理找出它们的大小及平行关系,进行转化,而PQ则比较麻烦,没有一个现成的平面可以将其放进去,如果想把PQ转化成BC及B1C1的话,可以联想到向量进行转化,然后再由A、B、C及A1、B1、C1分别共线,设定比例,再代入解决.
点评:此题将平面向量的基本定理运用到立体几何中的四点共面问题,是个不错的方法,体现了知识之间的相互联系.

练习册系列答案
相关题目