题目内容
在斜三棱柱ABC-A1B1C1中，平面A1ACC1⊥平面ABC，AC⊥BC，A1B⊥C1C，AC=BC．（1）求证A1A⊥A1C；
（2）若A1A=A1C，求二面角B-A1C-B1的余弦值．
考点：与二面角有关的立体几何综合题,空间中直线与直线之间的位置关系
专题：计算题,证明题
分析：（1）由A1A⊥BC，A1A⊥A1B证明A1A⊥平面A1BC，进而证明A1A⊥A1C；（2）通过空间直角坐标系中向量的运算求余弦值．
解答：
解：（1）∵平面A1ACC1⊥平面ABC，AC⊥BC，
∴BC⊥平面A1ACC1，
∴A1A⊥BC，
∵A1B⊥C1C，A1A∥CC1
∴A1A⊥A1B，
∴A1A⊥平面A1BC，
∴A1A⊥A1C；
（Ⅱ）建立如图所示的坐标系C-xyz．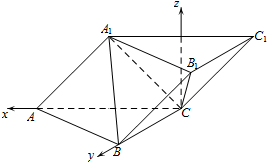
设AC=BC=2，
∵A1A=A1C，
则A（2，0，0），B（0，2，0），A1（1，0，1），C（0，0，0）．
=（0，2，0），
=（1，0，1），
=
=（-2，2，0）．
设
=（a，b，c）为面BA1C的一个法向量，则
•
=
•
=0，
则
取a=1，
=（1，0，-1）．
同理，面A1CB1的一个法向量为
=（1，1，-1）．
∴cos＜
，
＞=
=
，
∴二面角B-A1C-B1的余弦值为
．
∴BC⊥平面A1ACC1，
∴A1A⊥BC，
∵A1B⊥C1C，A1A∥CC1
∴A1A⊥A1B，
∴A1A⊥平面A1BC，
∴A1A⊥A1C；
（Ⅱ）建立如图所示的坐标系C-xyz．
设AC=BC=2，
∵A1A=A1C，
则A（2，0，0），B（0，2，0），A1（1，0，1），C（0，0，0）．
| CB |
| CA1 |
| A1B1 |
| AB |
设
| n1 |
| n1 |
| CB |
| n1 |
| CA1 |
则
|
| n1 |
同理，面A1CB1的一个法向量为
| n2 |
∴cos＜
| n1 |
| n2 |
| ||||||||||||
|
| ||
| 3 |
∴二面角B-A1C-B1的余弦值为
| ||
| 3 |
点评：本题考查了线面垂直的判定定理，用到了面面垂直的定义，也考查了在空间直角坐标系中求角的方法，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
某市一公交线路某区间内共设置六个站点（如图所示），分别为A0，A1，A2，A3，A4，A5，现有甲、乙两人同时从A0站点上车，且他们中的每个人在站点Ai（i=1，2，3，4，5）下车是等可能的．则甲、乙两人不在同一站点下车的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=log3x的定义域是（ ）
| A、R | B、（0，+∞） |
| C、（1，+∞） | D、（3，+∞） |
如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AD=2AB=2，E是PB的中点．
如图，在直三棱柱ABC-A′B′C′中，平面A′BC⊥侧面A′ABB′．