题目内容
棱长为2的正方体ABCD-A1B1C1D1在空间直角坐标系中移动,但保持点A、B分别在X轴、y轴上移动,则点C1到原点O的最远距离为( )
分析:通过正方体与空间直角坐标系,按照要求放置,只有C1与AB和O在同一个平面时,点C1到原点O的才有最远距离,画出截面图形,利用图象求出C1的坐标,利用两点距离公式求出OC1的表达式,通过三角函数的变换,求出最大值.
解答: 解:由题意可知,C1与AB和O在同一个平面时,C1到O的距离比较大,如图:设∠BAO=α,则C1坐标为(2
解:由题意可知,C1与AB和O在同一个平面时,C1到O的距离比较大,如图:设∠BAO=α,则C1坐标为(2
sinα,2sinα+2
cosα),
|OC1|=
=
=
,其中tanθ=
,
显然|OC1|≤
=4,
故选D.
 解:由题意可知,C1与AB和O在同一个平面时,C1到O的距离比较大,如图:设∠BAO=α,则C1坐标为(2
解:由题意可知,C1与AB和O在同一个平面时,C1到O的距离比较大,如图:设∠BAO=α,则C1坐标为(2| 2 |
| 2 |
|OC1|=
(2
|
=
10-2cos2α+4
|
=
| 10+6sin(2α-θ) |
| ||
| 4 |
显然|OC1|≤
| 16 |
故选D.
点评:本题考查空间想象能力,转化思想的应用,三角函数的化简求值,考查计算能力.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
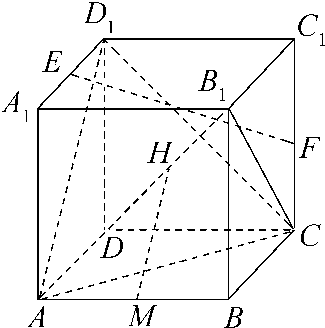 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F、M、H分别为A1D1、CC1、AB、DB1的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F、M、H分别为A1D1、CC1、AB、DB1的中点.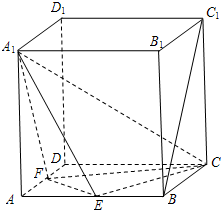 (2007•静安区一模)(文)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别是棱AB、AD的中点.求:
(2007•静安区一模)(文)如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E、F分别是棱AB、AD的中点.求: