题目内容
已知函数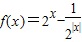 .
.(Ⅰ)若f(x)=2,求x的值;
(Ⅱ)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
【答案】分析:(I)当x≤0时得到f(x)=0而f(x)=2,所以无解;当x>0时解出f(x)=2求出x即可;
(II)由 t∈[1,2]时,3tf(2t)+mf(t)≥0恒成立得到,得到f(t)= ,代入得到m的范围即可.
,代入得到m的范围即可.
解答:解:(Ⅰ)当x≤0时f(x)=0,
当x>0时, ,
,
有条件可得, ,
,
即22x-2×2x-1=0,解得 ,∵2x>0,∴
,∵2x>0,∴ ,∴
,∴ .
.
(Ⅱ)当t∈[1,2]时, ,
,
即m(22t-1)≥-(24t-1).∵22t-1>0,∴m≥-(22t+1).
∵t∈[1,2],∴-(1+22t)∈[-17,-5],
故m的取值范围是[-5,+∞).
点评:本题主要考查了函数恒成立问题.属于基础题.恒成立问题多需要转化,因为只有通过转化才能使恒成立问题等到简化;转化过程中往往包含着多种数学思想的综合运用,同时转化过程更提出了等价的意识和要求.
(II)由 t∈[1,2]时,3tf(2t)+mf(t)≥0恒成立得到,得到f(t)=
 ,代入得到m的范围即可.
,代入得到m的范围即可.解答:解:(Ⅰ)当x≤0时f(x)=0,
当x>0时,
 ,
,有条件可得,
 ,
,即22x-2×2x-1=0,解得
 ,∵2x>0,∴
,∵2x>0,∴ ,∴
,∴ .
.(Ⅱ)当t∈[1,2]时,
 ,
,即m(22t-1)≥-(24t-1).∵22t-1>0,∴m≥-(22t+1).
∵t∈[1,2],∴-(1+22t)∈[-17,-5],
故m的取值范围是[-5,+∞).
点评:本题主要考查了函数恒成立问题.属于基础题.恒成立问题多需要转化,因为只有通过转化才能使恒成立问题等到简化;转化过程中往往包含着多种数学思想的综合运用,同时转化过程更提出了等价的意识和要求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. .
. .
. .
. .
. .
. ,
,