题目内容
某厂生产某种产品的年固定成本为 万元,每生产
万元,每生产 千件,需另投入成本为
千件,需另投入成本为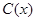 .当年产量不足
.当年产量不足 千件时,
千件时, (万元).当年产量不小于
(万元).当年产量不小于 千件时,
千件时, (万元).每件商品售价为
(万元).每件商品售价为 万元.通过市场分析,该厂生产的商品能全部售完.
万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
【答案】
(1)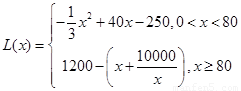 ;
;
(2)当产量为100 千件时,该厂在这一商品中所获利润最大,最大利润为1000 万元.
【解析】
试题分析:(1)根据题意分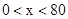 时,
时,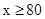 时,分别确定函数的解析式,得到分段函数以
时,分别确定函数的解析式,得到分段函数以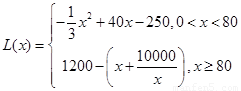 ;
;
(2)分别确定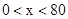 时,,
时,,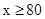 时,函数的最大值,并加以比较.确定函数的最大值时,应用了二次函数的性质及基本不等式.
时,函数的最大值,并加以比较.确定函数的最大值时,应用了二次函数的性质及基本不等式.
试题解析:
(1) 因为每件商品售价为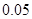 万元,则
万元,则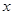 千件商品销售额为0.05×1000x万元,依题意得:
千件商品销售额为0.05×1000x万元,依题意得:
当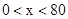 时,
时,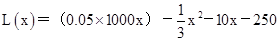
=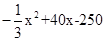 2分
2分
当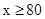 时,
时,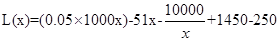
=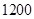 -
-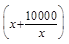 .
4分
.
4分
以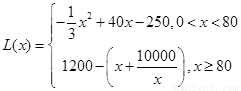 6分
6分
(2)当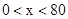 时,
时,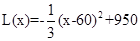 .
.
此时,当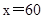 时,
时,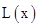 取得最大值
取得最大值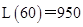 万元.
9分
万元.
9分
当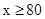 时,
时,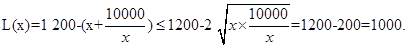
此时,当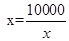 时,即
时,即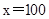 时,
时,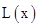 取得最大值1000万元.
12分
取得最大值1000万元.
12分
∵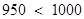
所以,当产量为100 千件时,该厂在这一商品中所获利润最大,最大利润为1000万元. 13分
考点:函数应用问题,分段函数,二次函数的性质,基本不等式.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 当年产量不足80千件时,
当年产量不足80千件时,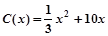 (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时, (万元).通过市场分析,若每件售价为500元时,该厂当年生产该产品能全部销售完.
(万元).通过市场分析,若每件售价为500元时,该厂当年生产该产品能全部销售完. (万元)关于年产量x(千件)的函数解析式;
(万元)关于年产量x(千件)的函数解析式; 当年产量不足80千件时,
当年产量不足80千件时,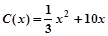 (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时, (万元).通过市场分析,若每件售价为500元时,该厂当年生产该产品能全部销售完.
(万元).通过市场分析,若每件售价为500元时,该厂当年生产该产品能全部销售完. (万元)关于年产量x(千件)的函数解析式;
(万元)关于年产量x(千件)的函数解析式; 万元,每生产
万元,每生产 (
( )千件,需另投入成本为
)千件,需另投入成本为 ,当年产量不足
,当年产量不足 千件时,
千件时, (万元);当年产量不小于
(万元);当年产量不小于 (万元).通过市场分析,若每千件售价为
(万元).通过市场分析,若每千件售价为 万元时,该厂年内生产该商品能全部销售完.
万元时,该厂年内生产该商品能全部销售完.  (万元)关于年产量
(万元)关于年产量