题目内容
已知 ,函数
,函数 的零点从小到大依次为
的零点从小到大依次为 ,
, .
.
(Ⅰ)若 (
( ),试写出所有的
),试写出所有的 值;
值;
(Ⅱ)若 ,
, ,
, ,求证:
,求证:  ;
;
(Ⅲ)若 ,
, ,
, ,试把数列
,试把数列 的前
的前 项及
项及 按从小到大的顺序排列。(只要求写出结果).
按从小到大的顺序排列。(只要求写出结果).
(Ⅰ) ;(Ⅱ)见解析;(Ⅲ)见解析
;(Ⅱ)见解析;(Ⅲ)见解析
【解析】
试题分析:(Ⅰ) ,
, ,
, ,
, ,
,
所以 ;(Ⅱ)
;(Ⅱ) ,
, 在
在 上单调递增,当
上单调递增,当 时,由(Ⅰ)知,
时,由(Ⅰ)知, ,
, 即
即 所以
所以 ,再利用数学归纳法证明即可,显然当
,再利用数学归纳法证明即可,显然当 时,命题成立,假设
时,命题成立,假设 时命题成立,即
时命题成立,即 ⑴
⑴
当 时,由式⑴得
时,由式⑴得 即
即 ,当
,当 时,命题也成立,所以
时,命题也成立,所以 ;(Ⅲ)同第二问也可用数学归纳法得到.
;(Ⅲ)同第二问也可用数学归纳法得到.
试题解析:(Ⅰ) ,
, ,
, ,
,
 ,
,
所以 3分
3分
(Ⅱ) ,
, 在
在 上单调递增,当
上单调递增,当 时,
时,
 , 1分
, 1分
由(Ⅰ)知, ,
, ,
,
即 2分
2分
所以 ①
①
下面用数学归纳法证明
由式①知, ,所以
,所以 ,
,
即 ,所以,当
,所以,当 时,命题成立
时,命题成立
假设 时命题成立,即
时命题成立,即
 ②
②
当 时,由式②得
时,由式②得

即
当 时,命题也成立,
时,命题也成立,
所以 7分
7分
(Ⅲ) ,
, 在R上单调递减,由于
在R上单调递减,由于  ,所以
,所以
 ,即
,即 ,可推出
,可推出
 ,即
,即
进而可得 ,
,
即 ,又可得
,又可得

即 ,所以用数学归纳法易证
,所以用数学归纳法易证
 3分
3分
考点:数学归纳法

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在R上是单调递减的奇函数,则下列关系式成立的是( )
在R上是单调递减的奇函数,则下列关系式成立的是( ) B.
B.
 D.
D.
 的实数根个数为 .
的实数根个数为 . 上任意一点,点Q的坐标为(4a,a+3),则PQ长度的最小值为 .
上任意一点,点Q的坐标为(4a,a+3),则PQ长度的最小值为 . .
. 的最小正周期及单调减区间;
的最小正周期及单调减区间; ,
, ,求
,求 的值.
的值.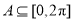 ,集合
,集合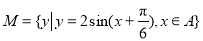 ,若
,若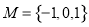 ,则不同集合A的个数是
,则不同集合A的个数是 表示平面区域为
表示平面区域为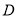 ,在区域
,在区域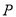 ,则点
,则点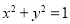 内的概率为 .
内的概率为 . 的周长是
的周长是 ,且
,且 ,则顶点
,则顶点 的轨迹方程是
的轨迹方程是


 K]
K]