题目内容
(本小题满分12分)
已知函数f(x)=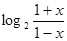 。
。
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性,并证明;
(3)判断函数f(x)在定义域上的单调性,并用定义证明。
已知函数f(x)=
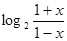 。
。(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性,并证明;
(3)判断函数f(x)在定义域上的单调性,并用定义证明。
(1)x∈(-1,1)
(2)函数f(x)是奇函数。
(3)函数f(x)=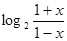 在(-1,1)上是增函数.
在(-1,1)上是增函数.
(2)函数f(x)是奇函数。
(3)函数f(x)=
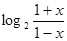 在(-1,1)上是增函数.
在(-1,1)上是增函数.试题分析:解:(1)由
 >0,解得-1<x<1,所以f(x)的定义域是(-1,1) 3分
>0,解得-1<x<1,所以f(x)的定义域是(-1,1) 3分证明:(2)由(1)知x∈(-1,1)
又因为f(-x)=
 =
= =
= =-
=-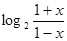 =-f(x).
=-f(x).所以函数f(x)是奇函数。 6分
(3)设-1<x<x<1,
f(x)-f(x)=
 -
- =
=
因为1-x>1-x>0;1+ x>1+ x>0,
所以
 >1. 所以
>1. 所以 >0.
>0.所以函数f(x)=
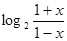 在(-1,1)上是增函数.
在(-1,1)上是增函数. 点评:解决的关键是利用奇偶性定义和单调性的定义来证明函数的性质,属于基础题。

练习册系列答案
相关题目
 的定义域是 .
的定义域是 .  的函数是 .
的函数是 .



 的定义域是
的定义域是 ,则实数
,则实数 的取值范围是( )
的取值范围是( )



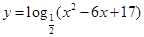 的值域是 .
的值域是 . 的定义域是 。
的定义域是 。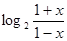 。
。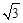 sin ax cos ax+2 cos2 ax的周期为π,其中a>0.
sin ax cos ax+2 cos2 ax的周期为π,其中a>0.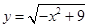 的值域为( )
的值域为( )