题目内容
若不等式(a-2)x2+2(a-2)x-4<0对一切x∈R恒成立,试确定实数a的取值范围.
当a=2时,原不等式变形为-4<0,恒成立,即a=2满足条件;
当a≠2时,要使不等式(a-2)x2+2(a-2)x-4<0对一切x∈R恒成立,
则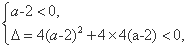 
化简得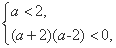
解得-2<a<2.
综上所述,实数a的取值范围是{a|-2<a≤2}.
练习册系列答案
相关题目
题目内容
若不等式(a-2)x2+2(a-2)x-4<0对一切x∈R恒成立,试确定实数a的取值范围.
当a=2时,原不等式变形为-4<0,恒成立,即a=2满足条件;
当a≠2时,要使不等式(a-2)x2+2(a-2)x-4<0对一切x∈R恒成立,
则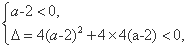
化简得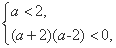
解得-2<a<2.
综上所述,实数a的取值范围是{a|-2<a≤2}.
B.
D．1
时,
f'(x)>0,则函数y=f(x)-sin x在[-2π,2π]上的零点个数为 . 
和p.
,求p的值;
=(1,-2),
=(a,-1),
=(-b,0),a>0,b>0,O为坐标原点,若A,B,C三点共线,则
+
的最小值为 . 