题目内容
求函数y=sin2x+2sinxcosx+3cos2x的最小值，并求使y取最小值时x的集合．
当{
}时，函数取得最小值，最小值为2-
}时，函数取得最小值，最小值为2-由y=sin2x+2sinxcosx+3cos2x
得：y=2sinxcosx+2cos2x+1 ="sin2x+cos2x" +2
=
+2
=
+2
当
=" " 
即x=
时，
y=2-
所以当{}时，函数取得最小值，最小值为2-.
得：y=2sinxcosx+2cos2x+1 ="sin2x+cos2x" +2
=
+2=
+2当
=" " 即x= 时， y=2-所以当{
}时，函数取得最小值，最小值为2-.
练习册系列答案
相关题目
=2,求下列各式的值：
;
;
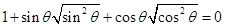成立,则角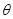
不可能是 ( )
，试用含
的式子表示
．
，
，
，
，且
∥
，则
＝ .
，则
等于（ ）
B 
C 
D 
，则
的值为
