Question

（本小题满分12分）在棱锥中，平面平面，是的中点，

.

（1）求证：；

（2）求三棱锥的高。

Answer 1

（1）详见解析；（2）三棱锥F—ADE的高为1.

【解析】

试题分析：（1）要证,只要证平面；一方面可以通过证明 平面 证明 ；另一方面可以利用勾股定理证明为直角三角形，从而证明；

（2）利用等积变换法，设三棱锥的高为 ，因为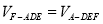

所以， ,从而求得的值.

试题解析：（1）证明：∵DC⊥平面ABC，∴DC⊥AF，

又∵AB=AC ，F是BC的中点，所以AF⊥BC，

∴AF⊥平面BCD

所以AF⊥FE 2分

在△DEF中，

所以DF⊥EF， 5分

∴EF⊥平面AFD，故FE⊥AD 6分

（2） 【解析】
由（1）知DF⊥EF，所以S△DEF=DF×EF= 7分

（或：又DC⊥平面ABC，EB⊥平面ABC，所以DC∥EB

因为S△DEF=S梯形BCDE-S△DCF- S△BEF= 7分）

在△DEF中，

所以，由余弦定理得 9分

所以S△DEA=

设三棱锥F—ADE的高h，则S△DEF×AF=

所以h=1，即三棱锥F—ADE的高为1 12分

考点：1、空间直线与平面的位置关系；2、棱锥的体积；3、等积变换的思想；4、余弦定理.