题目内容
复数z1=
思路分析:z1+z2是虚数,则虚部不为0,把z1+z2化为a+bi的形式.?
解:z1+z2=![]() -2+(m2
-2+(m2
∵z1+z2为虚数,?
∴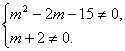
∴m≠5,m≠-3,m≠-2.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
题目内容
复数z1=
思路分析:z1+z2是虚数,则虚部不为0,把z1+z2化为a+bi的形式.?
解:z1+z2=![]() -2+(m2
-2+(m2
∵z1+z2为虚数,?
∴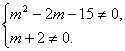
∴m≠5,m≠-3,m≠-2.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案