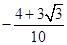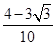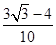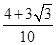题目内容
如图所示,点 是圆
是圆 上的三点,线段
上的三点,线段 与线段
与线段 交于圆内一点,若
交于圆内一点,若 ,则( )
,则( )
A. ; ; | B. ; ; |
C. ; ; | D. ; ; |
B
解析试题分析:如果记得结论,“ 三点共线,
三点共线, 是直线
是直线 外一点,
外一点, ,
, 三点共线
三点共线 .”则本题可很快得出结论,设
.”则本题可很快得出结论,设 是
是 与
与 的交点,且
的交点,且 ,则
,则 ,而
,而 ,显然
,显然 ,又
,又 ,
, ,故
,故 .如果记不得这个结论,则直接从等式
.如果记不得这个结论,则直接从等式 入手,
入手, ,而
,而 ,因此
,因此 ,所以
,所以 .
.
考点:向量数量积的性质.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
定义: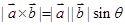 ,其中
,其中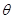 为向量
为向量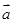 与
与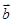 的夹角,若
的夹角,若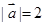 ,
,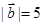 ,
,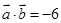 ,则
,则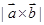 等于( )
等于( )
A. | B.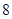 | C. 或 或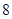 | D.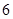 |
下列说法中:⑴若向量 ,则存在实数
,则存在实数 ,使得
,使得 ;
;
⑵非零向量 ,若满足
,若满足 ,则
,则
⑶与向量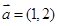 ,
, 夹角相等的单位向量
夹角相等的单位向量
⑷已知 ,若对任意
,若对任意 ,
,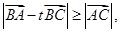 则
则 一定为锐角三角形。
一定为锐角三角形。
其中正确说法的序号是( )
| A.(1)(2) | B.(1)(3) | C.(2)(4) | D.(2) |
已知 ,则
,则 =( )
=( )
A. | B. | C. | D. |
如图,菱形 的边长为
的边长为 ,
, ,
, 为
为 的中点,若
的中点,若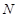 为菱形内任意一点(含边界),则
为菱形内任意一点(含边界),则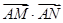 的最大值为( )
的最大值为( )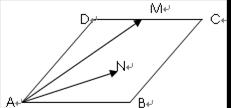
A. | B. | C.9 | D.6 |
若函数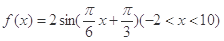 的图象与x轴交于点
的图象与x轴交于点 ,过点
,过点 的直线
的直线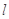 与函数
与函数 的图象交于
的图象交于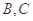 两点,则
两点,则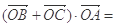 ( )
( )
A.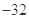 | B.16 | C.32 | D.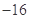 |
若向量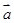 与
与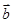 的夹角为120°,且
的夹角为120°,且 ,则有( )
,则有( )
A.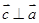 | B.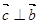 | C.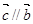 | D.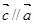 |
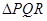 是圆O的内接正三角形,当
是圆O的内接正三角形,当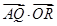 的取值范围是( )
的取值范围是( )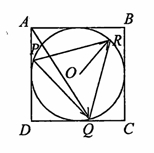
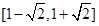

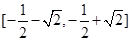
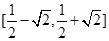
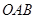 中,点
中,点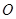 为原点,点
为原点,点 的坐标是
的坐标是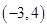 ,点
,点 在第一象限,向量
在第一象限,向量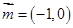 ,记向量
,记向量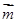 与向量
与向量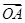 的夹角为
的夹角为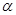 ,则
,则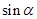 的值为( )
的值为( )