题目内容
集合A={x|x2-x-2≤0，x∈R}，集合B={x|
}，则A∩B=
- A.（-∞，3]∪[1，+∞）
- B.[
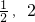] - C.（]
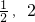- D.[-3，1]
C
分析：首先化简集合A和B，然后根据交集的定义得出结果．
解答：∵集合A={x|x2-x-2≤0，x∈R}={x|-1≤x≤2}
集合B={x|}={x|x≤-3或x＞
}
∴A∩B=（，2]
故选：C．
点评：此题考查了交集的定义，正确化简集合A和B是解题的关键，属于基础题．
分析：首先化简集合A和B，然后根据交集的定义得出结果．
解答：∵集合A={x|x2-x-2≤0，x∈R}={x|-1≤x≤2}
集合B={x|
}={x|x≤-3或x＞}∴A∩B=（
，2]故选：C．
点评：此题考查了交集的定义，正确化简集合A和B是解题的关键，属于基础题．
练习册系列答案
相关题目