题目内容
【题目】设a为实数，记函数f（x）=a 
+ 
+ 
的最大值为g（a）．
（1）设t= + ，求t的取值范围，并把f（x）表示为t的函数m（t）；
（2）求g（a）；
（3）试求满足g（a）=g（ 
）的所有实数a．
【答案】
（1）解：∵t= 
+ 
，要使t有意义，必须1+x≥0且1﹣x≥0，即﹣1≤x≤1．
∵t2=2+2 
∈[2，4]，且t≥0…①，
∴t的取值范围是[ 
，2]．
由①得： = 
t2﹣1，∴m（t）=a（ t2﹣1）+t= at2+t﹣a，t∈[ ，2]
（2）解：由题意知g（a）即为函数m（t）= at2+t﹣a，t∈[ ，2]的最大值，
∵直线t=﹣ 
是抛物线m（t）= at2+t﹣a的对称轴，∴可分以下几种情况进行讨论：
1°当a＞0时，函数y=m（t），t∈[ ，2]的图象是开口向上的抛物线的一段，
由t=﹣ ＜0知m（t）在t∈[ ，2]上单调递增，故g（a）=m（2）=a+2；
2°当a=0时，m（t）=t，在t∈[ ，2]上单调递增，有g（a）=2；
3°当a＜0时，函数y=m（t），t∈[ ，2]的图象是开口向下的抛物线的一段，
若t=﹣ ∈（0， ]即a≤﹣ 
时，g（a）=m（ ）= ，
若t=﹣ ∈（ ，2]即a∈（﹣ ，﹣ ]时，g（a）=m（﹣ ）=﹣a﹣ 
，
若t=﹣ ∈（2，+∞）即a∈（﹣ ，0）时，g（a）=m（2）=a+2．
综上所述，有g（a）=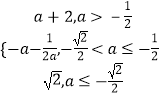 
（3）解：当a＞﹣ 时，g（a）=a+2＞ 
＞
a∈（﹣ ，﹣ ]时，﹣a∈[ ， ]，﹣a≠﹣
g（a）=﹣a﹣ ＞2 
=
∴a＞﹣ 时，g（a）＞
当a＞0时， ＞0，由g（a）=g（ ）可得 
，∴a=1；
当a＜0时，a =1，∴a≤﹣1或 ≤﹣1
∴g（a）= 或g（ 
）=
要使g（a）=g（ ），只需a≤﹣ ， ≤﹣ ，∴ 
综上，满足g（a）=g（ ）的所有实数a 或a=1
【解析】（1）令t= + ，由1+x≥0且1﹣x≥0，得﹣1≤x≤1，进而得m（t）的解析式．（2）由题意知g（a）即为函数m（t）= at2+t﹣a，t∈[ ，2]的最大值，分a＞0、a=0、a＜0三种情况利用函数的单调性求出函数f（x）的最大值为g（a）；（3）分类讨论，求得g（a）的范围，即可求得满足g（a）=g（ ）的所有实数a．
