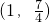题目内容
方程log3x+2x=6的根必定属于区间( )
| A.(-2,1) | B.(1,
| C.(
| D.(
|
当x=3时,f(3)=log33-6+2×3=1>0
当x=2时,f(2)=log32-6+2×2=log32-2<0
当x=
时,f(
)=log3
-6+2×
=log3
<0
即f(
)•f(3)<0
又∵函数f(x)=log3x-6+2x为连续函数
故函数f(x)=log3x-6+2x的零点一定位于区间(
,3)
故选D
当x=2时,f(2)=log32-6+2×2=log32-2<0
当x=
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 6 |
即f(
| 5 |
| 2 |
又∵函数f(x)=log3x-6+2x为连续函数
故函数f(x)=log3x-6+2x的零点一定位于区间(
| 5 |
| 2 |
故选D

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
方程log3x+2x=6的根必定属于区间( )
| A、(-2,1) | ||||
B、(1,
| ||||
C、(
| ||||
D、(
|