题目内容
设正实数a、b、c、x、y,且a、b、c为常数,x、y为变量,若x+y=c,则
+
的最大值是( )
| ax |
| by |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
分析:先假设x=csin2t,y=ccos2t,t∈(0,π/2),然后代入到
+
中,再由辅角公式可求得最大值.
| ax |
| by |
解答:解:设x=csin2t,y=ccos2t,t∈(0,π/2)
则
+
=
sint+
cost
=
sin(t+α)其中tanα=
当取t=
-α时,有最大值
故选A.
则
| ax |
| by |
| ac |
| bc |
=
| (a+b)c |
| ||
|
当取t=
| π |
| 2 |
| (a+b)c |
故选A.
点评:本题主要考查辅角公式的应用和参数方程的假设.考查基础知识的综合应用.高考中基础知识占据百分之80的比例,平时一定要注意基础知识的积累.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 ,比较
,比较 与
与 的大小.
的大小.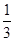 B.
B.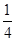 C.
C.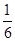 D.
D.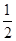
 +
+ 的最大值是( )
的最大值是( )


