题目内容
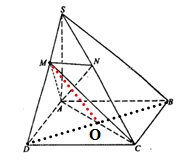
如图,在四棱锥S-ABCD中,底面ABCD是矩形,SA 底面ABCD,SA=AD,点M是SD的中点,AN
底面ABCD,SA=AD,点M是SD的中点,AN SC且交SC于点N.
SC且交SC于点N.
(Ⅰ)求证:SB∥平面ACM;
(Ⅱ)求证:平面SAC 平面AMN.
平面AMN.
(Ⅰ)见解析;(Ⅱ)见解析.
解析试题分析:(Ⅰ) 连接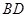 ,交
,交 于点
于点 ,连接
,连接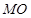 ,证明
,证明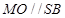 ,依据直线与平面平行的判定定理可知,
,依据直线与平面平行的判定定理可知,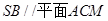 ;(Ⅱ)先由已知条件得到
;(Ⅱ)先由已知条件得到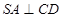 和
和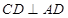 ,依据直线与平面垂直的判定定理证得
,依据直线与平面垂直的判定定理证得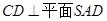 ,再由
,再由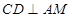 和
和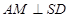 ,依据直线与平面垂直的判定定理证得
,依据直线与平面垂直的判定定理证得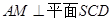 ,从而有
,从而有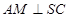 ,结合已知条件
,结合已知条件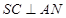 ,依据直线与平面垂直的判定定理证得
,依据直线与平面垂直的判定定理证得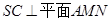 ,再依据平面与平面垂直的判定定得到
,再依据平面与平面垂直的判定定得到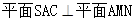 .
.
试题解析:(Ⅰ)连接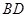 ,交
,交 于点
于点 ,连接
,连接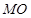 ,
,
∵ 为矩形,
为矩形,
∴ 为
为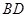 中点,又
中点,又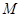 为
为 中点,∴
中点,∴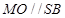 .
.
∵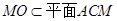 ,
,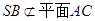 ,∴
,∴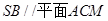 .
.
(Ⅱ)∵ ,∴
,∴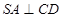 ,
,
∵ 为矩形,∴
为矩形,∴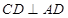 ,且
,且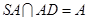 ,
,
∴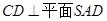 ,∴
,∴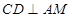 ,
,
∵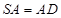 ,
,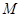 为
为 的中点,∴
的中点,∴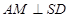 ,且
,且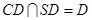 ,
,
∴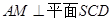 ,
,
∴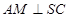 ,又∵
,又∵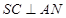 ,且
,且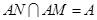 , ∴
, ∴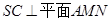 ,
,
∵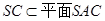 ,∴
,∴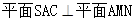 .
.
考点:1.直线与平面平行的判定定理;2.直线与平面垂直的判定定理;3.直线与平面垂直的性质定理;4.平面与平面垂直的判定定理

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
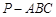 中,点
中,点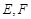 分别是棱
分别是棱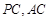 的中点.
的中点.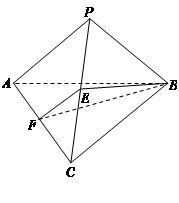
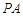 //平面
//平面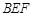 ;
;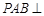 平面
平面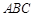 ,
,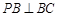 ,求证:
,求证: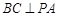 .
.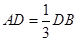 ,点C为圆O上一点,且
,点C为圆O上一点,且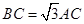 .点P在圆O所在平面上的正投影为点D,PD=DB.
.点P在圆O所在平面上的正投影为点D,PD=DB.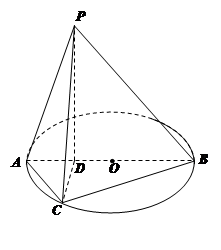
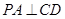 ;
;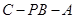 的余弦值.
的余弦值.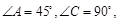
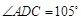 ,
,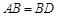 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD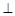 平面BDC,设点F为棱AD的中点.
平面BDC,设点F为棱AD的中点.

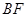 与平面ACD所成角的余弦值.
与平面ACD所成角的余弦值. 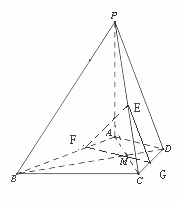
 为正方形,平面
为正方形,平面 为等腰梯形,
为等腰梯形, ,
,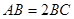 ,
, ,
, .
.
 平面
平面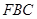 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值. 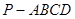 中,底面为直角梯形,
中,底面为直角梯形,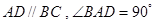 ,
,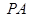 垂直于底面
垂直于底面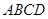 ,
,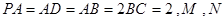 分别为
分别为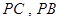 的中点.
的中点.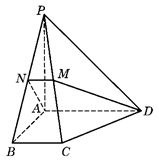
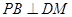 ;
; 到平面
到平面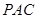 的距离.
的距离. 中,底面
中,底面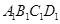 是正方形,
是正方形, 是
是 的中点,
的中点,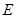 是棱
是棱 上任意一点.
上任意一点.
 ;
; ,求
,求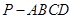 中,底面
中,底面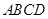 为菱形,
为菱形,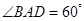 ,
,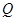 为
为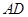 的中点.
的中点.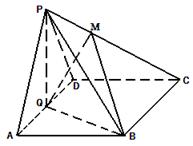
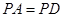 ,求证:平面
,求证:平面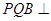 平面
平面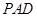 ;
;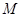 在线段
在线段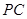 上,
上,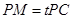 ,试确定
,试确定 的值,使
的值,使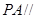 平面
平面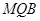 .
.