题目内容
函数f(x)=sin x- cos x(x∈[-π,0])的单调递增区间是
cos x(x∈[-π,0])的单调递增区间是
- A.[-π,-
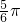 ]
] - B.[-
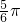 ,-
,- ]
] - C.[-
 ,0]
,0] - D.[-
 ,0]
,0]
D
分析:先利用两角和公式对函数解析式化简整理,进而根据正弦函数的单调性求得答案.
解答:f(x)=sin x- cos x=2sin(x-
cos x=2sin(x- ),
),
因x- ∈[-
∈[- π,-
π,- ],
],
故x- ∈[-
∈[- π,-
π,- ],
],
得x∈[- ,0],
,0],
故选D
点评:本题主要考查了正弦函数的单调性.对于正弦函数的单调性、奇偶性、对称性等特点应熟练掌握.
分析:先利用两角和公式对函数解析式化简整理,进而根据正弦函数的单调性求得答案.
解答:f(x)=sin x-
 cos x=2sin(x-
cos x=2sin(x- ),
),因x-
 ∈[-
∈[- π,-
π,- ],
],故x-
 ∈[-
∈[- π,-
π,- ],
],得x∈[-
 ,0],
,0],故选D
点评:本题主要考查了正弦函数的单调性.对于正弦函数的单调性、奇偶性、对称性等特点应熟练掌握.

练习册系列答案
相关题目
 函数f(x)=sin(ωx+?)(x∈R,ω>0,0≤?<2π)的部分图象如图,则
函数f(x)=sin(ωx+?)(x∈R,ω>0,0≤?<2π)的部分图象如图,则