题目内容
如图,Rt△ABC的斜边AB的平面α内,AC,BC与平面α所成角分别为30°和45°,求△ABC所在平面与α所成的二面角.
解:作CC′⊥平面α,C′为垂足,作C′D⊥AB于D,连结CD.
∴CD⊥AB.
∴∠CDC′是所求二面角的平面角.
由CC′⊥α可知,∠CAC′=30°,∠CBC′=45°.设CC′=h,在Rt△CC′A和Rt△CC′B中,AC=2h,BC=
h,
又∵AC⊥BC,∴AB=
h,
CD=(AC·BC)∶AB=
h.
∴sin∠CDC′=
.
又∠CDC′为锐角,∴∠CDC′=60°.
∴△ABC所在平面与α所成的二面角为60°.
练习册系列答案
相关题目
如图Rt△ABC中，AB=AC=1，以点C为一个焦点作一个椭圆，使这个椭圆的另一个焦点在AB边上，且这个椭圆过A、B两点，则这个椭圆的焦距长为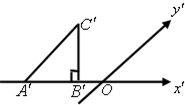
如图，△ABC的斜二侧直观图为等腰Rt△A'B'C'，其中A'B'=2，则△ABC的面积为（ ）
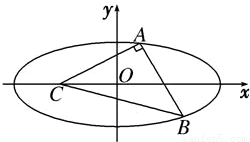如图Rt△ABC中，AB=AC=1，以点C为一个焦点作一个椭圆，使这个椭圆的另一个焦点在AB边上，且这个椭圆过A、B两点，则这个椭圆的焦距长为 ．