题目内容
下列命题正确的是
①平面内α的两条相交直线分别平行于平面β内的两条相交直线,则平面α平行于平面β;
②两个平面分别经过两条平行直线,则这两个平面互相平行;
③若平面α平行于平面β,平面β平行于平面r,则平面α平行于平面r;
④若α⊥r,β⊥r则α∥β;
⑤α⊥β,β⊥r则α⊥r.
- A.①②⑤
- B.②③④
- C.①③
- D.①③④
C
分析:对于①根据面面平行的判定定理进行判定,对于②可列举反例,如三棱柱的两个侧面,对于③根据面面平行的性质进行判定,对于④列举反例,如正方体过同一顶点的三个平面,对于⑤α与r可能平行,从而得到结论.
解答:①平面内α的两条相交直线分别平行于平面β内的两条相交直线,则平面α平行于平面β,根据面面平行的判定定理可知正确;
②两个平面分别经过两条平行直线,则这两个平面互相平行,不正确,如三棱柱的两个侧面;
③若平面α平行于平面β,平面β平行于平面r,则平面α平行于平面r,根据面面平行的性质可知正确;
④若α⊥r,β⊥r则α∥β,不正确,如正方体过同一顶点的三个平面;
⑤α⊥β,β⊥r则α⊥r.不正确,α与r可能平行;
故选C
点评:本题主要考查了空间中直线与平面之间的位置关系,以及考查学生空间想象能力,逻辑思维能力,是中档题.
分析:对于①根据面面平行的判定定理进行判定,对于②可列举反例,如三棱柱的两个侧面,对于③根据面面平行的性质进行判定,对于④列举反例,如正方体过同一顶点的三个平面,对于⑤α与r可能平行,从而得到结论.
解答:①平面内α的两条相交直线分别平行于平面β内的两条相交直线,则平面α平行于平面β,根据面面平行的判定定理可知正确;
②两个平面分别经过两条平行直线,则这两个平面互相平行,不正确,如三棱柱的两个侧面;
③若平面α平行于平面β,平面β平行于平面r,则平面α平行于平面r,根据面面平行的性质可知正确;
④若α⊥r,β⊥r则α∥β,不正确,如正方体过同一顶点的三个平面;
⑤α⊥β,β⊥r则α⊥r.不正确,α与r可能平行;
故选C
点评:本题主要考查了空间中直线与平面之间的位置关系,以及考查学生空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
下列关于向量的命题,正确的是( )
| A、零向量是长度为零,且没有方向的向量 | ||||||||
B、若
| ||||||||
C、若
| ||||||||
| D、在同一平面上,单位向量有且仅有一个 |
 中,棱长为4,
中,棱长为4, 是BC的中点,
是BC的中点, 在线段
在线段 上运动(
上运动( 、
、
 平面
平面 ,
,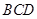 交于点Q,
交于点Q, 面
面
 ②Q点一定在直线DM上 ③
②Q点一定在直线DM上 ③
 中,棱长为4,
中,棱长为4, 是BC的中点,
是BC的中点, 在线段
在线段 上运动(
上运动( 、
、
 平面
平面 ,
, 交于点Q,给出下列命题:
交于点Q,给出下列命题: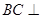 面
面
 ②Q点一定在直线DM上 ③
②Q点一定在直线DM上 ③

 中,棱长为4,
中,棱长为4, 是BC的中点,
是BC的中点, 在线段
在线段 上运动(
上运动( 、
、
 平面
平面 ,
,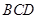 交于点Q,
交于点Q, 面
面
 ②Q点一定在直线DM上 ③
②Q点一定在直线DM上 ③