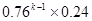题目内容
甲、乙两名篮球队员独立地轮流投篮,直到某人投中为止.甲投中的概率为0.4,乙为0.6,分别求出甲、乙两人投篮次数的分布列(假设甲先投).
解析:设ξ=“甲投篮次数”,η=“乙投篮次数”,
设事件A=“前k-1次均不中,第k次甲投中”;B=“前k-1次均不中,第k次甲仍不中而乙投中”;C=“前k次均不中,第k+1次甲投中”.则A、B、C互斥,所求分布列为:
P(ξ=k)=P(A)+P(B)=(0.6)k-1×(0.4)k-1×0.4+(0.6)k×(0.4)k-1×0.6=0.76×(0.24)k-1,k=1,2,3,…;
P=(η=0)=0.4;
P(η=k)=P(B)+P(C)=(0.6)k×(0.4)k-1×0.6+(0.6)k×(0.4)k×0.4=0.456×(0.24)k-1,k=1,2,3….

练习册系列答案
相关题目
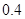 ,乙投中的概率为
,乙投中的概率为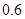 ,而且不受其他次投篮结果的影响,设投篮的轮数为
,而且不受其他次投篮结果的影响,设投篮的轮数为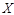 ,若甲先投,则
,若甲先投,则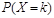 等于( )
等于( )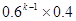 B. 0.24k-1×0.4
C.
B. 0.24k-1×0.4
C. 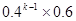 D.
D.