题目内容
13.数列{an}满足a1=0,an+1=$\frac{{a}_{n}-\sqrt{3}}{\sqrt{3}{a}_{n}+1}$,n∈N*,求a100,S2015.分析 由递推式,分别计算a2,a3,a4,…,可得an+3=an.即可得出数列的周期为3,进而可得所求a100,S2015的值.
解答 解:∵a1=0,an+1=$\frac{{a}_{n}-\sqrt{3}}{\sqrt{3}{a}_{n}+1}$(n∈N*),
∴a2=$\frac{-\sqrt{3}}{0+1}$=-$\sqrt{3}$,a3=$\frac{-\sqrt{3}-\sqrt{3}}{1-3}$=$\sqrt{3}$,
a4=$\frac{\sqrt{3}-\sqrt{3}}{1+3}$=0,…,
∴an+3=an.
∴a1+a2+a3=0,
∴a100=a3×33+1=a1=0;
S2015=(a1+a2+a3)×671+a1+a2=-$\sqrt{3}$.
点评 本题考查了递推关系、数列的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
4.若y=log2(x+a)的反函数的图象经过点P(-1,0),则实数a的值为( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
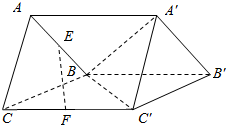 如图,三棱柱ABC-A′B′C′,E,F分别是AB,CC′的中点,过EF作一个平面和面A′BC′相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)
如图,三棱柱ABC-A′B′C′,E,F分别是AB,CC′的中点,过EF作一个平面和面A′BC′相交,并找到交线,写出作法.(注意:交线必须是由两个确定的点的连线)