题目内容
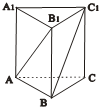
在正三棱柱ABC-A1B1C1中,AB=
,若AB1⊥BC1,则正三棱柱的体积为( )
| 2 |
A.
| B.
| C.
| D.
|

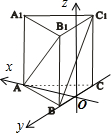
因为几何体是正三棱柱,所以作AO⊥BC于O作如图所示的空间直角坐标系,
设棱柱的高为h,所以A(
,0,0),B(0,
,0),B1(0,
,h),C1(0,-
,h),
∵AB1⊥BC1,∴
•
=0,
即(-
,
,h)•(0,-
,h)=0,
解得h=1,
正三棱柱的体积为:
×
×
×1=
.
故选A.
设棱柱的高为h,所以A(
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∵AB1⊥BC1,∴
| AB1 |
| BC1 |
即(-
| ||
| 2 |
| ||
| 2 |
| 2 |
解得h=1,
正三棱柱的体积为:
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
故选A.


练习册系列答案
相关题目
 如图,在正三棱柱ABC-A1B1C1中,AA1=AB,D是AC的中点.
如图,在正三棱柱ABC-A1B1C1中,AA1=AB,D是AC的中点.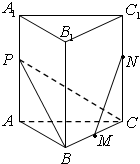 如图,在正三棱柱ABC-A1B1C1中,所有棱的长度都是1,M是BC边的中点,P是AA1边上的点,且
如图,在正三棱柱ABC-A1B1C1中,所有棱的长度都是1,M是BC边的中点,P是AA1边上的点,且 如图,在正三棱柱ABC-A'B'C'中,AB=2,若二面角C'-AB-C的大小为60°,则点C到平面ABC'的距离为
如图,在正三棱柱ABC-A'B'C'中,AB=2,若二面角C'-AB-C的大小为60°,则点C到平面ABC'的距离为