题目内容
13.cos$\frac{2π}{7}$cos$\frac{4π}{7}$cos$\frac{6π}{7}$=$\frac{1}{8}$.分析 首先将原式变形为cos$\frac{2π}{7}$cos$\frac{4π}{7}$cos(π-$\frac{π}{7}$)的形式,观察角度关系恰好是二倍角关系,所以分子、分母同时乘8sin$\frac{π}{7}$,3次运用正弦的二倍角公式化简求值.
解答 解:原式=cos$\frac{2π}{7}$cos$\frac{4π}{7}$cos(π-$\frac{π}{7}$)=-$\frac{8sin\frac{π}{7}cos\frac{π}{7}cos\frac{2π}{7}cos\frac{4π}{7}}{8sin\frac{π}{7}}$=-$\frac{4sin\frac{2π}{7}cos\frac{2π}{7}cos\frac{4π}{7}}{8sin\frac{π}{7}}$=-$\frac{2sin\frac{4π}{7}cos\frac{4π}{7}}{8sin\frac{π}{7}}$=-$\frac{sin\frac{8π}{7}}{8sin\frac{π}{7}}$=-$\frac{-sin\frac{π}{7}}{8sin\frac{π}{7}}$=$\frac{1}{8}$;
故答案为:$\frac{1}{8}$.
点评 本题考查了三角函数式的化简求值;关键是发现角度的关系,巧配二倍角公式.

练习册系列答案
相关题目
4.若曲线y2=2px(p>0)上有且只有一个点到其焦点的距离为1,则p的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,直线l过焦点F,且斜率为k,则直线l与双曲线C的左、右两支都相交的充要条件是( )
| A. | k>-$\frac{b}{a}$ | B. | k<$\frac{b}{a}$ | C. | k>$\frac{b}{a}$或k<-$\frac{b}{a}$ | D. | -$\frac{b}{a}$<k<$\frac{b}{a}$ |
9.已知区域D:$\left\{\begin{array}{l}y≥2\\ x+y-2≥0\\ x-y-1≤0.\end{array}\right.$若圆C:(x-a)2+(y-2)2=2与区域D有公共点,则实数a的取值范围是( )
| A. | [-1,5] | B. | [-2,2] | C. | [-2,5] | D. | [-1,2] |
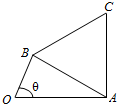 已知函数f(x)=sinωx(0<ω<2)在区间,[0,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3}$,$\frac{2π}{3}$]单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4ω}{3}-cosB-cosC}{cosA}$.
已知函数f(x)=sinωx(0<ω<2)在区间,[0,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3}$,$\frac{2π}{3}$]单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4ω}{3}-cosB-cosC}{cosA}$.