题目内容
若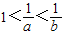 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )A.logab>logba
B.|logab+logba|>2
C.(logba)2<1
D.|logab|+|logba|>|logab+logba|
【答案】分析:若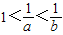 ,则易得0<b<a<1,则可以根据指数的性质:logab>1,0<logba<1,及logab•logba=1,对四个答案逐一进行分析,易得答案
,则易得0<b<a<1,则可以根据指数的性质:logab>1,0<logba<1,及logab•logba=1,对四个答案逐一进行分析,易得答案
解答:解法一:(常规做法)
∵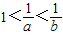 ,
,
∴0<b<a<1,
则logab>1,0<logba<1,logab•logba=1,
∴logab>logba,故A正确.
由基本不等式得:logab+logba≥2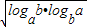 =2,故B正确.
=2,故B正确.
∴0<(logba)2<1,故C正确.
|logab|+|logba|<|logab+logba|,故D错误.
解法二:(特殊值代入法)
∵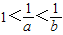 ,
,
∴0<b<a<1,
不妨令b= ,a=
,a=
则logab=2,logba=
易得A,B,C均正确,只有D错误
故选D
点评:特殊值代入法,是解选择题和填空题常用的方法之一,使用时要注意,其方法是通过设题中某个未知量为特殊值,从而通过简单的运算,得出最终答案的一种方法.这个特殊值应该满足的条件:首先,无论这个量的值是多少,对最终结果所要求的量的值没有影响;其次,这个量应该要跟最终结果所要求的量有相对紧密的联系;最后,这个量在整个题干中给出的等量关系是一个不可或缺的量.
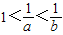 ,则易得0<b<a<1,则可以根据指数的性质:logab>1,0<logba<1,及logab•logba=1,对四个答案逐一进行分析,易得答案
,则易得0<b<a<1,则可以根据指数的性质:logab>1,0<logba<1,及logab•logba=1,对四个答案逐一进行分析,易得答案解答:解法一:(常规做法)
∵
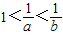 ,
,∴0<b<a<1,
则logab>1,0<logba<1,logab•logba=1,
∴logab>logba,故A正确.
由基本不等式得:logab+logba≥2
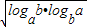 =2,故B正确.
=2,故B正确.∴0<(logba)2<1,故C正确.
|logab|+|logba|<|logab+logba|,故D错误.
解法二:(特殊值代入法)
∵
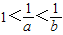 ,
,∴0<b<a<1,
不妨令b=
 ,a=
,a=
则logab=2,logba=

易得A,B,C均正确,只有D错误
故选D
点评:特殊值代入法,是解选择题和填空题常用的方法之一,使用时要注意,其方法是通过设题中某个未知量为特殊值,从而通过简单的运算,得出最终答案的一种方法.这个特殊值应该满足的条件:首先,无论这个量的值是多少,对最终结果所要求的量的值没有影响;其次,这个量应该要跟最终结果所要求的量有相对紧密的联系;最后,这个量在整个题干中给出的等量关系是一个不可或缺的量.

练习册系列答案
相关题目

 (单位:kg)与身高
(单位:kg)与身高 (单位:cm)
具有线性相关关系,根据一组样本数据(
(单位:cm)
具有线性相关关系,根据一组样本数据( ,
,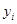 )(i=1,2,…,n),用最小二乘法建立的回归方程为
)(i=1,2,…,n),用最小二乘法建立的回归方程为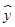 =0.85x-85.71,则下列结论中不正确的是 ( )
=0.85x-85.71,则下列结论中不正确的是 ( )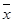 ,
,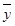 )
)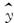 =0.85x-85.71,则下列结论中不正确的是( ).
=0.85x-85.71,则下列结论中不正确的是( ).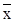 ,
,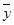 )
) =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是 ,
,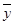 )
) =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是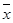 ,
,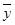 )
)