题目内容
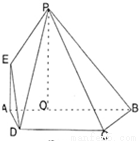
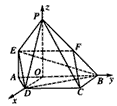
如图,PO⊥平面ABCD,点O在AB上,EA∥PO,四边形ABCD为直角梯形,BC⊥AB,BC=CD=BO=PO,EA=AO=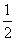 CD,
CD,
(Ⅰ)求证:PE⊥平面PBC;
(Ⅱ)直线PE上是否存在点M,使DM∥平面PBC,若存在,求出点M;若不存在,说明理由;
(Ⅲ)求二面角E-BD-A的余弦值。
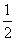 CD,
CD,(Ⅰ)求证:PE⊥平面PBC;
(Ⅱ)直线PE上是否存在点M,使DM∥平面PBC,若存在,求出点M;若不存在,说明理由;
(Ⅲ)求二面角E-BD-A的余弦值。
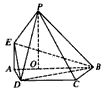
解:(Ⅰ) ∵EA∥OP,AO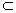 平面ABP, 平面ABP,∴点A,B,P,E共面, ∵PO⊥平面ABCD,PO 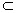 平面PEA, 平面PEA,∴平面PEAB⊥平面ABCD, ∵BC 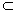 平面ABCD,BC⊥AB,平面PFAB∩平面ABCD=AB, 平面ABCD,BC⊥AB,平面PFAB∩平面ABCD=AB,∴BC⊥平面PEAB,PE⊥BC, 由平面几何知识知PE⊥PB, 又BC∩PB=B, ∴PE⊥平面PBC。 (Ⅱ)点E即为所求的点,即点M与点E重合, 取PB的中点F,连接EF,CF,DE, 由平面几何知识知EF∥AB,且EF=DC, ∴四边形DCEF为平行四边形,所以DE∥CF, ∵CF在平面PBC内,DE不在平面PBC内, ∴DE∥平面PBC。 |
|
| (Ⅲ)由已知可知四边形BCDO是正方形,显然OD,OB,OP两两垂直, 如图建立空间直角坐标系,设DC=1, 则  , ,设平面BDE的一个法向量为  ,并设 ,并设 =(x,y,z), =(x,y,z),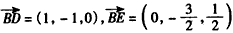 , ,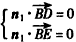 ,即 ,即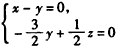 ,取y=1,则x=1,z=3, ,取y=1,则x=1,z=3,从而  , ,取平面ABD的一个法向量为 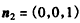 , ,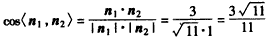 , ,故二面角E-BD-A的余弦值为 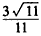 。 。 |
 |

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
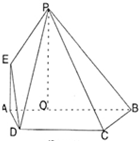 (2010•广东模拟)如图,PO⊥ABCD,点O在AB上,EA∥PO,四边形ABCD为直角梯形,BC⊥AB,BC=CD=BO=PO,EA=AO=
(2010•广东模拟)如图,PO⊥ABCD,点O在AB上,EA∥PO,四边形ABCD为直角梯形,BC⊥AB,BC=CD=BO=PO,EA=AO=

 CD
CD