题目内容
(本题满分16分)
已知直线![]() 与函数
与函数![]() 的图象相切于点
的图象相切于点![]() ,且
,且![]() 与函数
与函数
![]()
![]() 的图象也相切.
的图象也相切.
(Ⅰ)求直线![]() 的方程及
的方程及![]() 的值;
的值;
(Ⅱ)设![]() ,若
,若![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
解:(Ⅰ)∵![]() ,直线
,直线![]() 是函数
是函数![]() 的图象在点
的图象在点![]() 处的切线,
处的切线,
∴其斜率为![]()
∴直线![]() 的方程为
的方程为![]() . ……………3分
. ……………3分
又因为直线![]() 与
与![]() 的图象相切,
的图象相切,
由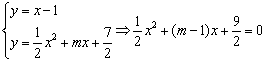 ,
,
得![]() (
(![]() 不合题意,舍去) ……………6分
不合题意,舍去) ……………6分
(Ⅱ)方法一:![]()
由![]() 恒成立,
恒成立,
得![]() 恒成立 ……………8分
恒成立 ……………8分
设![]() ,则
,则![]() ……………9分
……………9分
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
于是,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
故![]() 的最大值为
的最大值为![]() ……………11分
……………11分
要使![]() 恒成立,只需
恒成立,只需![]() ∴a的取值范围为
∴a的取值范围为![]() ……………12分
……………12分
方法二:由(Ⅰ)知,![]()
∴![]()
![]()
……………8分
(i)若![]() 时,令
时,令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() ,
,
故![]() 在
在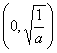 上单调递减,在
上单调递减,在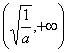 上单调递增
上单调递增
故![]() 在
在![]() 上的最小值为
上的最小值为![]()
要使解得![]() 恒成立,只需
恒成立,只需![]() ,得
,得![]() …………12分
…………12分
(ii)若![]() ,
,![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,
故不可能![]() 恒成立 ……………15分
恒成立 ……………15分
综上所述,![]() 即a的取值范围为
即a的取值范围为![]() ……………16分
……………16分

练习册系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在