题目内容
已知函数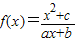 为奇函数,f(1)<f(3),且不等式
为奇函数,f(1)<f(3),且不等式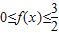 的解集是[-2,-1]∪[2,4]
的解集是[-2,-1]∪[2,4](1)求a,b,c.
(2)是否存在实数m使不等式
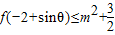 对一切θ∈R成立?若存在,求出m的取值范围;若不存在,请说明理由.
对一切θ∈R成立?若存在,求出m的取值范围;若不存在,请说明理由.
【答案】分析:(1)根据函数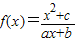 为奇函数,则f(-x)=-f(x),构造方程可得b值,由不等式
为奇函数,则f(-x)=-f(x),构造方程可得b值,由不等式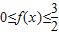 的解集是[-2,-1]∪[2,4],根据±2均为不等式的解,可得c值,根据f(1)<f(3),结合函数单调性,及不等式解集的端点是对应方程的根,求出a值.
的解集是[-2,-1]∪[2,4],根据±2均为不等式的解,可得c值,根据f(1)<f(3),结合函数单调性,及不等式解集的端点是对应方程的根,求出a值.
(2)根据(1)中函数的单调性,结合奇函数在对称区间上单调性相同,可得f(x)在(-∞,0)上也是增函数,将不等式恒成立转化为函数的最值问题后,构造关于m的不等式,可得答案.
解答:解:(1)∵ ,
,
∴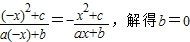 .…(1分)
.…(1分)
不等式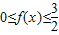 的解集中包含2和-2,
的解集中包含2和-2,
∴f(2)≥0,f(-2)=-f(2)≥0,
即得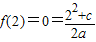 ,所以c=-4…(2分)
,所以c=-4…(2分)
∵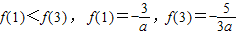 ,
,
∴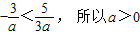 .…(3分)
.…(3分)
当a>0时,在(0,+∞)上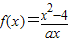 是增函数
是增函数
在(0,+∞)内任取x1,x2,且x1<x2,那么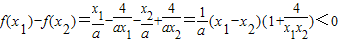
即 …(5分)
…(5分)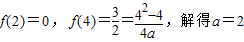 .
.
综上所述: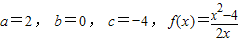 …(6分)
…(6分)
(2)∵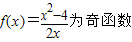 ,
,
∴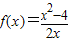 在(-∞,0)上也是增函数.…(7分)
在(-∞,0)上也是增函数.…(7分)
又-3≤-2+sinθ≤-1,
∴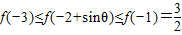 ,
,
而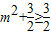 ,
,
所以,m为任意实数时,不等式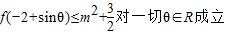 …(12分)
…(12分)
点评:本题是函数奇偶性,单调性,函数恒成立问题及不等式方程函数关系的综合应用,其中根据已知求出函数的解析式难度比较大,也是解答本题的关键.
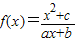 为奇函数,则f(-x)=-f(x),构造方程可得b值,由不等式
为奇函数,则f(-x)=-f(x),构造方程可得b值,由不等式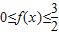 的解集是[-2,-1]∪[2,4],根据±2均为不等式的解,可得c值,根据f(1)<f(3),结合函数单调性,及不等式解集的端点是对应方程的根,求出a值.
的解集是[-2,-1]∪[2,4],根据±2均为不等式的解,可得c值,根据f(1)<f(3),结合函数单调性,及不等式解集的端点是对应方程的根,求出a值.(2)根据(1)中函数的单调性,结合奇函数在对称区间上单调性相同,可得f(x)在(-∞,0)上也是增函数,将不等式恒成立转化为函数的最值问题后,构造关于m的不等式,可得答案.
解答:解:(1)∵
 ,
,∴
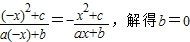 .…(1分)
.…(1分)不等式
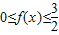 的解集中包含2和-2,
的解集中包含2和-2,∴f(2)≥0,f(-2)=-f(2)≥0,
即得
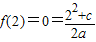 ,所以c=-4…(2分)
,所以c=-4…(2分)∵
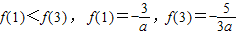 ,
,∴
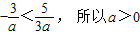 .…(3分)
.…(3分)当a>0时,在(0,+∞)上
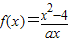 是增函数
是增函数在(0,+∞)内任取x1,x2,且x1<x2,那么
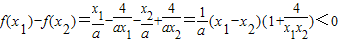
即
 …(5分)
…(5分)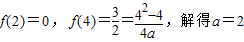 .
.综上所述:
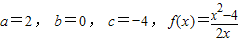 …(6分)
…(6分)(2)∵
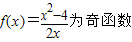 ,
,∴
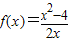 在(-∞,0)上也是增函数.…(7分)
在(-∞,0)上也是增函数.…(7分)又-3≤-2+sinθ≤-1,
∴
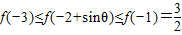 ,
,而
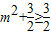 ,
,所以,m为任意实数时,不等式
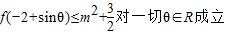 …(12分)
…(12分)点评:本题是函数奇偶性,单调性,函数恒成立问题及不等式方程函数关系的综合应用,其中根据已知求出函数的解析式难度比较大,也是解答本题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
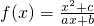 为奇函数,f(1)=-3,且对任意x∈[π,2π],f(sinx-1)≥0恒成立,f(cosx+3)≥0恒成立.
为奇函数,f(1)=-3,且对任意x∈[π,2π],f(sinx-1)≥0恒成立,f(cosx+3)≥0恒成立.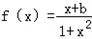 为奇函数.
为奇函数.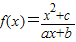 为奇函数,f(1)<f(3),且不等式
为奇函数,f(1)<f(3),且不等式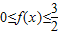 的解集是[-2,-1]∪[2,4]
的解集是[-2,-1]∪[2,4]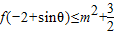 对一切θ∈R成立?若存在,求出m的取值范围;若不存在,请说明理由.
对一切θ∈R成立?若存在,求出m的取值范围;若不存在,请说明理由.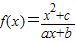 为奇函数,f(1)=-3,且对任意x∈[π,2π],f(sinx-1)≥0恒成立,f(cosx+3)≥0恒成立.
为奇函数,f(1)=-3,且对任意x∈[π,2π],f(sinx-1)≥0恒成立,f(cosx+3)≥0恒成立.