题目内容
设f(x)是R上的偶函数,且在(-∞,0)上为减函数,若x1<0,且x1+x2>0,则
- A.f(x1)>f(x2)
- B.f(x1)=f(x2)
- C.f(x1)<f(x2)
C
分析:先利用x1<0且x1+x2>0把自变量都转化到区间(-∞,0)上,再根据f(x)在(-∞,0)上是增函数,可得函数值大小关系,再根据偶函数性质即可求出答案.
解答:因为x1<0且x1+x2>0,故0>x1>-x2;
因为函数f(x)在(-∞,0)上是减函数,所以有f(x1)<f(-x2).
又因为f(x)是R上的偶函数,所以f(-x2)=f(x2).
所以有f(x1)<f(x2).
故选C.
点评:本题主要考查抽象函数的单调性和奇偶性.抽象函数是相对于给出具体解析式的函数来说的,它虽然没有具体的表达式,但是有一定的对应法则,满足一定的性质,这种对应法则及函数的相应的性质是解决问题的关键.抽象函数的抽象性赋予它丰富的内涵和多变的思维价值,可以考查类比猜测,合情推理的探究能力和创新精神.
分析:先利用x1<0且x1+x2>0把自变量都转化到区间(-∞,0)上,再根据f(x)在(-∞,0)上是增函数,可得函数值大小关系,再根据偶函数性质即可求出答案.
解答:因为x1<0且x1+x2>0,故0>x1>-x2;
因为函数f(x)在(-∞,0)上是减函数,所以有f(x1)<f(-x2).
又因为f(x)是R上的偶函数,所以f(-x2)=f(x2).
所以有f(x1)<f(x2).
故选C.
点评:本题主要考查抽象函数的单调性和奇偶性.抽象函数是相对于给出具体解析式的函数来说的,它虽然没有具体的表达式,但是有一定的对应法则,满足一定的性质,这种对应法则及函数的相应的性质是解决问题的关键.抽象函数的抽象性赋予它丰富的内涵和多变的思维价值,可以考查类比猜测,合情推理的探究能力和创新精神.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
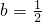 ,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.
,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由. ,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.
,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.