题目内容
19.已知函数f(x)=(1)当a=![]() 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2)若对任意x![]() [1,+
[1,+![]() ),f(x)>0恒成立,试求实数a的取值范围.
),f(x)>0恒成立,试求实数a的取值范围.
19.解:
(1)当a=![]() 时,f(x)=x+
时,f(x)=x+![]() +2,
+2,
∵f(x)在区间[1,+∞)上为增函数,
∴f(x)在区间[1,+∞)上的最小值为f(1)=![]() .
.
(2)解法一:在区间 [1,+∞)上,
f(x)=![]() >0恒成立
>0恒成立![]() x2+2x+a>0恒成立.
x2+2x+a>0恒成立.
设y=x2+2x+a,x∈[1,+∞),
y=x2+2x+a=(x+1)2+a-1递增,∴当x=1时,ymin=3+a.
于是当且仅当ymin=3+a>0时,函数f(x)>0恒成立,故a>-3.
解法二:f(x)=x+![]() ,x∈[1,+∞),
,x∈[1,+∞),
当a≥0时,函数f(x)的值恒为正,
当a<0时,函数f(x)递增,
故当x=1时,f(x)min=3+a.
于是当且仅当f(x)min=3+a>0时,
函数f(x)>0恒成立,故a>-3.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
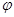 )(ω>0,0<
)(ω>0,0<
 =
= ,且a∈(0,
,且a∈(0, ),求f(a)的值.
),求f(a)的值. -a
-a +x(a>0).
+x(a>0). =
= ,求f(x)图像在x=1处的切线的方程;
,求f(x)图像在x=1处的切线的方程; 的极大值和极小值分别为m,n,证明:
的极大值和极小值分别为m,n,证明: .
.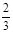 与x=1时都取得极值.
与x=1时都取得极值. ,若f(x)存在零点,则实数a的取值范围
,若f(x)存在零点,则实数a的取值范围