题目内容
如图,半圆O的直径MN=2,OA=2,B为半圆上任意一点,以AB为一边作正三角形ABC,问B在什么位置时,四边形OACB面积最大?最大面积是多少?

答案:
解析:
解析:
解:设∠AOB=θ,由余弦定理知AB2=OA2+OB2-2OA·OB·cosθ=5-4cosθ ∴S△ABC= S△AOB= ∴S四边形OACB= 当θ= 最大值为
|

练习册系列答案
相关题目
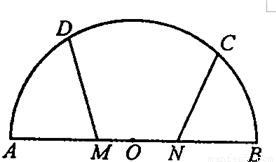
 如图,AB是半圆O的直径,C,D是弧AB三等分点,M,N是线段AB的三等分点,若OA=6,则
如图,AB是半圆O的直径,C,D是弧AB三等分点,M,N是线段AB的三等分点,若OA=6,则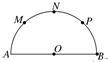 如图,已知AB是半圆O的直径,AB=8,M、N、P是将半圆圆周四等分的三个分点
如图,已知AB是半圆O的直径,AB=8,M、N、P是将半圆圆周四等分的三个分点 (2013•成都模拟)如图,AB是半圆O的直径,C、D是弧AB的三等分点,M、N是线段AB的三等分点,若OA=6,则
(2013•成都模拟)如图,AB是半圆O的直径,C、D是弧AB的三等分点,M、N是线段AB的三等分点,若OA=6,则
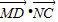 的值是( )
的值是( )