题目内容
已知函数f(x)=x2-alnx(a∈R).(Ⅰ)若a=2,求证:f(x)在(1,+∞)上是增函数;
(Ⅱ)求f(x)在[1,+∞)上的最小值.
【答案】分析:(Ⅰ)要证函数在(1,+∞)上是增函数,只需要证明其导数大于0即可;求导函数先研究函数的单调性,确定极值,从而确定函数的最值,分类讨论是解题的关键.
(Ⅱ)先求出f(x)的导数,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,求出极值、最值即可.
解答:证明:(Ⅰ)当a=2时,f(x)=x2-2lnx,当x∈(1,+∞)时,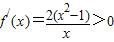 ,所以f(x)在(1,+∞)上是增函数; …(5分)
,所以f(x)在(1,+∞)上是增函数; …(5分)
(Ⅱ)解: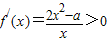 ,
,
当a≤0时,f′(x)>0,f(x)在[1,+∞)上单调递增,最小值为f(1)=1.
当a>0,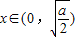 时,f(x)单调递减;当
时,f(x)单调递减;当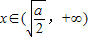 时,f(x)单调递增.
时,f(x)单调递增.
若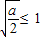 ,即0<a≤2时,f(x)在[1,+∞)上单调递增,又f(1)=1,,所以f(x)在[1,+∞)上的最小值为1.
,即0<a≤2时,f(x)在[1,+∞)上单调递增,又f(1)=1,,所以f(x)在[1,+∞)上的最小值为1.
若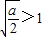 ,即a>2时,f(x)在
,即a>2时,f(x)在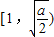 上单调递减;在
上单调递减;在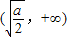 上单调递增.
上单调递增.
又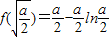 ,所以f(x)在[1,+∞)上的最小值为
,所以f(x)在[1,+∞)上的最小值为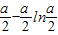 .
.
综上,当a≤2时,f(x)在[1,+∞)上的最小值为1;
当a>2时,f(x)在[1,+∞)上的最小值为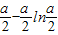 .…(13分)
.…(13分)
点评:利用导数研究函数的单调性比用函数单调性的定义要方便,但应注意f′(x)>0(或f′(x)<0)仅是f(x)在某个区间上为增函数(或减函数)的充分条件,在(a,b)内可导的函数f(x)在(a,b)上递增(或递减)的充要条件应是f′(x)≥0[或f′(x)≤0],x∈(a,b)恒成立,且f′(x)在(a,b)的任意子区间内都不恒等于0,这就是说,函数f(x)在区间上的增减性并不排斥在区间内个别点处有f′(x0)=0,甚至可以在无穷多个点处f′(x0)=0,只要这样的点不能充满所给区间的任何一个子区间,因此,在已知函数f(x)是增函数(或减函数)求参数的取值范围时,应令f′(x)≥0[或f′(x)≤0]恒成立,解出参数的取值范围(一般可用不等式恒成立理论求解),然后检验参数的取值能否使f′(x)恒等于0,若能恒等于0,则参数的这个值应舍去,若f′(x)不恒为0,则由f′(x)≥0[或f′(x)≤0]恒成立解出的参数的取值范围确定.
(Ⅱ)先求出f(x)的导数,根据f′(x)>0求得的区间是单调增区间,f′(x)<0求得的区间是单调减区间,求出极值、最值即可.
解答:证明:(Ⅰ)当a=2时,f(x)=x2-2lnx,当x∈(1,+∞)时,
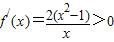 ,所以f(x)在(1,+∞)上是增函数; …(5分)
,所以f(x)在(1,+∞)上是增函数; …(5分)(Ⅱ)解:
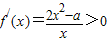 ,
,当a≤0时,f′(x)>0,f(x)在[1,+∞)上单调递增,最小值为f(1)=1.
当a>0,
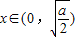 时,f(x)单调递减;当
时,f(x)单调递减;当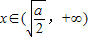 时,f(x)单调递增.
时,f(x)单调递增.若
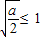 ,即0<a≤2时,f(x)在[1,+∞)上单调递增,又f(1)=1,,所以f(x)在[1,+∞)上的最小值为1.
,即0<a≤2时,f(x)在[1,+∞)上单调递增,又f(1)=1,,所以f(x)在[1,+∞)上的最小值为1.若
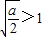 ,即a>2时,f(x)在
,即a>2时,f(x)在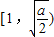 上单调递减;在
上单调递减;在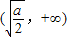 上单调递增.
上单调递增.又
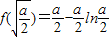 ,所以f(x)在[1,+∞)上的最小值为
,所以f(x)在[1,+∞)上的最小值为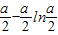 .
.综上,当a≤2时,f(x)在[1,+∞)上的最小值为1;
当a>2时,f(x)在[1,+∞)上的最小值为
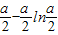 .…(13分)
.…(13分)点评:利用导数研究函数的单调性比用函数单调性的定义要方便,但应注意f′(x)>0(或f′(x)<0)仅是f(x)在某个区间上为增函数(或减函数)的充分条件,在(a,b)内可导的函数f(x)在(a,b)上递增(或递减)的充要条件应是f′(x)≥0[或f′(x)≤0],x∈(a,b)恒成立,且f′(x)在(a,b)的任意子区间内都不恒等于0,这就是说,函数f(x)在区间上的增减性并不排斥在区间内个别点处有f′(x0)=0,甚至可以在无穷多个点处f′(x0)=0,只要这样的点不能充满所给区间的任何一个子区间,因此,在已知函数f(x)是增函数(或减函数)求参数的取值范围时,应令f′(x)≥0[或f′(x)≤0]恒成立,解出参数的取值范围(一般可用不等式恒成立理论求解),然后检验参数的取值能否使f′(x)恒等于0,若能恒等于0,则参数的这个值应舍去,若f′(x)不恒为0,则由f′(x)≥0[或f′(x)≤0]恒成立解出的参数的取值范围确定.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|