题目内容
【题目】如图，建立平面直角坐标系xOy，x轴在地平面上，y轴垂直于地平面，单位长度为1千米．某炮位于坐标原点．已知炮弹发射后的轨迹在方程y＝kx－
(1＋k2)x2(k＞0)表示的曲线上，其中k与发射方向有关．炮的射程是指炮弹落地点的横坐标．
设在第一象限有一飞行物(忽略其大小)，其飞行高度为3.2千米，试问它的横坐标a不超过多少时，炮弹可以击中它？请说明理由．
【答案】详见解析.
【解析】试题分析：求炮弹击中目标时的横坐标的最大值，炮弹可击中目标存在k＞0，使3.2＝ka－
(1＋k2)a2成立，因为k＞0关于k的方程a2k2－20ak＋a2＋64＝0有正根判别式Δ＝(－20a)2－4a2(a2＋64)≥0解不等式得解.
试题解析：
因为a＞0，所以炮弹可击中目标存在k＞0，使3.2＝ka－
(1＋k2)a2成立关于k的方程a2k2－20ak＋a2＋64＝0有正根由韦达定理满足两根之和大于0，两根之积大于0，故只需判别式Δ＝(－20a)2－4a2(a2＋64)≥0a≤6.
所以当a不超过6(千米)时，可击中目标．
【题目】如图，四边形ABCD为菱形，G为AC与BD的交点，BE⊥平面ABCD，
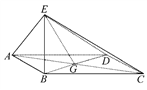
(1)证明：平面AEC⊥平面BED.
(2)若∠ABC=120°，AE⊥EC，三棱锥E-ACD的体积为
，求该三棱锥的侧面积.
【题目】近年来，我国电子商务蓬勃发展. 2016年“618”期间，某网购平台的销售业绩高达516亿元人民币，与此同时，相关管理部门推出了针对该网购平台的商品和服务的评价系统. 从该评价系统中选出200次成功交易，并对其评价进行统计，网购者对商品的满意率为0.6，对服务的满意率为0.75，其中对商品和服务都满意的交易为80次.
(Ⅰ) 根据已知条件完成下面的
列联表，并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”？
对服务满意 | 对服务不满意 | 合计 | |
对商品满意 | 80 | ||
对商品不满意 | |||
合计 | 200 |
(Ⅱ) 若将频率视为概率，某人在该网购平台上进行的3次购物中，设对商品和服务都满意的次数为随机变量
，求的分布列和数学期望
.
附：
（其中
为样本容量）
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运
会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度，选了某小区的100位居民调查结果统计如下：
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
（1）根据已有数据，把表格数据填写完整；
（2）能否在犯错误的概率不超过5％的前提下认为不同年龄与支持申办奥运无关?
（3）已知在被调查的年龄大于50岁的支持者中有5名女性，其中2位是女教师，现从这5名女性中随机抽取3人，求至多有1位教师的概率．
