题目内容
面积为S的平面凸四边形的第i条边的边长记为ai(i=1,2,3,4),此四边形内任一点P到第i条边的距离为hi(i=1,2,3,4),若
=
=
=
=k,则h1+2h2+3h3+4h4=
;根据以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为Hi(i=1,2,3,4),若
=
=
=
=k,则H1+2H2+3H3+4H4=( )
| a1 |
| 1 |
| a2 |
| 2 |
| a3 |
| 3 |
| a4 |
| 4 |
| 2s |
| k |
| S1 |
| 1 |
| S2 |
| 2 |
| S3 |
| 3 |
| S4 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:由
=
=
=
=k可得ai=ik,P是该四边形内任意一点,将P与四边形的四个定点连接,得四个小三角形,四个小三角形面积之和为四边形面积,即采用分割法求面积;同理对三棱值得体积可分割为5个已知底面积和高的小棱锥求体积.
| a1 |
| 1 |
| a2 |
| 2 |
| a3 |
| 3 |
| a4 |
| 4 |
解答:解:根据三棱锥的体积公式 V=
Sh
得:
S1H1+
S2H2+
S3H3+
S4H4=V,
即S1H1+2S2H2+3S3H3+4S4H4=3V,
∴H1+2H2+3H3+4H4=
,
即
(iHi)=
.
故选B.
| 1 |
| 3 |
得:
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
即S1H1+2S2H2+3S3H3+4S4H4=3V,
∴H1+2H2+3H3+4H4=
| 3V |
| K |
即
| 4 |
 |
| i=1 |
| 3V |
| K |
故选B.
点评:本题主要考查三棱锥的体积计算和运用类比思想进行推理的能力.解题的关键是理解类比推理的意义,掌握类比推理的方法.平面几何的许多结论,可以通过类比的方法,得到立体几何中相应的结论.当然,类比得到的结论是否正确,则是需要通过证明才能加以肯定的.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
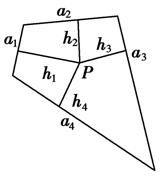
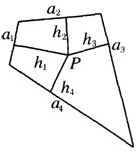 如图所示,面积为S的平面凸四边形的第i条边的边长记为ai(i=1,2,3,4),此四边形内任一点P到第i条边的距离记为hi(i=1,2,3,4),若
如图所示,面积为S的平面凸四边形的第i条边的边长记为ai(i=1,2,3,4),此四边形内任一点P到第i条边的距离记为hi(i=1,2,3,4),若
 =
= =
= =k,则
=k,则 (ihi)=
(ihi)=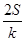 .类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为hi(i=1,2,3,4),若
.类比以上性质,体积为V的三棱锥的第i个面的面积记为Si(i=1,2,3,4),此三棱锥内任一点Q到第i个面的距离记为hi(i=1,2,3,4),若 B.
B.  C.
C.
 D.
D.

