题目内容
(本小题10分)已知向量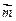 =(1+cosB,sinB)且与向量
=(1+cosB,sinB)且与向量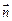 =(0,1)所成的角为
=(0,1)所成的角为 ,其中A、B、C为ΔABC的三个内角。
,其中A、B、C为ΔABC的三个内角。
(1)求角B的大小;(2)若AC=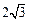 ,求ΔABC周长的最大值。
,求ΔABC周长的最大值。
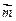 =(1+cosB,sinB)且与向量
=(1+cosB,sinB)且与向量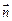 =(0,1)所成的角为
=(0,1)所成的角为 ,其中A、B、C为ΔABC的三个内角。
,其中A、B、C为ΔABC的三个内角。(1)求角B的大小;(2)若AC=
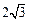 ,求ΔABC周长的最大值。
,求ΔABC周长的最大值。(1)B= 。(2)ΔABC的周长的最大值为
。(2)ΔABC的周长的最大值为 。
。
 。(2)ΔABC的周长的最大值为
。(2)ΔABC的周长的最大值为 。
。.解:法(1):①∵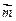 =(1+cosB,sinB)与
=(1+cosB,sinB)与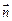 =(0,1)所成的角为
=(0,1)所成的角为
∴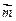 与向量
与向量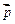 =(1,0)所成的角为
=(1,0)所成的角为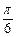
∴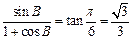 ,即
,即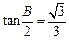 (2分)
(2分)
而B∈(0,π),∴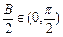 ,∴
,∴ ,∴B=
,∴B= 。 (4分)
。 (4分)
②令AB=c,BC=a,AC=b
∵B= ,∴b2=a2+c2-2accosB=a2+c2-ac=
,∴b2=a2+c2-2accosB=a2+c2-ac=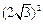 ,∵a,c>0。 (6分)
,∵a,c>0。 (6分)
∴a2+c2≥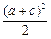 ,ac≤
,ac≤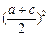 (当且仅当a=c时等号成立)
(当且仅当a=c时等号成立)
∴12=a2+c2-ac≥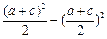
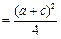 (8分)
(8分)
∴(a+c)2≤48,∴a+c≤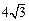 ,∴a+b+c≤
,∴a+b+c≤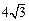 +
+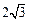 =
= (当且仅当a=c时取等号)
(当且仅当a=c时取等号)
故ΔABC的周长的最大值为 。 (10分)
。 (10分)
法2:(1)cos<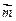 ,
,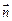 >=cos
>=cos
∴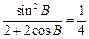 , (2分)
, (2分)
即2cos2B+cosB-1=0,∴cosB=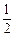 或cosB=-1(舍),而B∈(0,π),∴B=
或cosB=-1(舍),而B∈(0,π),∴B= (4分)
(4分)
(2)令AB=c,BC=a,AC=b,ΔABC的周长为 ,则
,则 =a+c+
=a+c+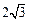
而a=b·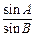 ,c=b·
,c=b·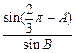 (2分)
(2分)
∴ =
=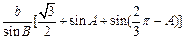 =
=
= (8分)
(8分)
∵A∈(0,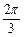 ),∴A-
),∴A-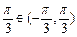 ,
,
当且仅当A= 时,
时,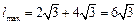 。 (10分)
。 (10分)
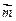 =(1+cosB,sinB)与
=(1+cosB,sinB)与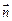 =(0,1)所成的角为
=(0,1)所成的角为
∴
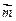 与向量
与向量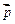 =(1,0)所成的角为
=(1,0)所成的角为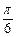
∴
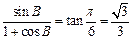 ,即
,即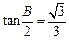 (2分)
(2分)而B∈(0,π),∴
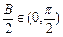 ,∴
,∴ ,∴B=
,∴B= 。 (4分)
。 (4分)②令AB=c,BC=a,AC=b
∵B=
 ,∴b2=a2+c2-2accosB=a2+c2-ac=
,∴b2=a2+c2-2accosB=a2+c2-ac=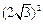 ,∵a,c>0。 (6分)
,∵a,c>0。 (6分)∴a2+c2≥
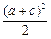 ,ac≤
,ac≤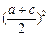 (当且仅当a=c时等号成立)
(当且仅当a=c时等号成立)∴12=a2+c2-ac≥
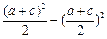
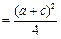 (8分)
(8分)∴(a+c)2≤48,∴a+c≤
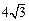 ,∴a+b+c≤
,∴a+b+c≤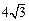 +
+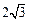 =
= (当且仅当a=c时取等号)
(当且仅当a=c时取等号)故ΔABC的周长的最大值为
 。 (10分)
。 (10分)法2:(1)cos<
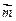 ,
,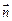 >=cos
>=cos
∴
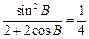 , (2分)
, (2分)即2cos2B+cosB-1=0,∴cosB=
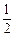 或cosB=-1(舍),而B∈(0,π),∴B=
或cosB=-1(舍),而B∈(0,π),∴B= (4分)
(4分)(2)令AB=c,BC=a,AC=b,ΔABC的周长为
 ,则
,则 =a+c+
=a+c+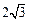
而a=b·
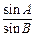 ,c=b·
,c=b·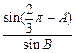 (2分)
(2分)∴
 =
=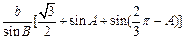 =
=
=
 (8分)
(8分)∵A∈(0,
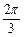 ),∴A-
),∴A-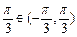 ,
,当且仅当A=
 时,
时,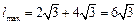 。 (10分)
。 (10分)
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 中,
中, ,
, .(10分)
.(10分) 的值; (Ⅱ)设
的值; (Ⅱ)设 ,求
,求 中,
中, 分别为角
分别为角 的对边,已知
的对边,已知 ,
,
 ,求
,求
 ,求
,求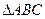 中,a=15,b=10,A=60°,则
中,a=15,b=10,A=60°,则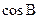 =( )
=( )

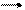 AB=a,
AB=a,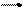 BC=b,
BC=b, CA=c,若a·(a+b
CA=c,若a·(a+b )<0,则△ABC是( )
)<0,则△ABC是( ) 角三角形
角三角形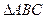 是锐角三角形,
是锐角三角形,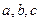 分
分 别是内角
别是内角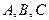 所对边长,且
所对边长,且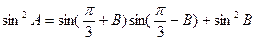
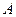 的值;
的值;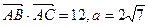 ,求
,求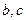 (其中
(其中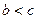 )。
)。 中,
中, 则
则 的值等于__________,
的值等于__________, 的取值范围为___________.
的取值范围为___________. 
 .
.