题目内容
设四面体四个面的面积分别为S1，S2，S3，S4，它们的最大值为S，记λ=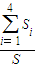
，则λ一定满足（ ）A．2＜λ≤4
B．3＜λ＜4
C．2.5＜λ≤4.5
D．3.5＜λ＜5.5
【答案】分析：根据棱锥的结构特征，结合四面体的四个面的面积分别为S1，S2，S3，S4，其中它们的最大值为S，可得当S1=S2=S3=S4时，
取最大值4，当“棱锥的高趋近0时，
趋近2，进而得到答案．
解答：解：由题意，当S1=S2=S3=S4时，
取最大值4；
棱锥的高趋近0时，S1+S2+S3+S4的值趋近2，
∴S1+S2+S3+S4＞2S，
∴
＞2
∴2＜λ≤4
故选A．
点评：本题考查的知识点是棱锥的结构特征，其中根据已知条件和棱锥的结构特征，确定面积的最值是关键．
取最大值4，当“棱锥的高趋近0时，趋近2，进而得到答案．解答：解：由题意，当S1=S2=S3=S4时，
取最大值4；棱锥的高趋近0时，S1+S2+S3+S4的值趋近2，
∴S1+S2+S3+S4＞2S，
∴
＞2∴2＜λ≤4
故选A．
点评：本题考查的知识点是棱锥的结构特征，其中根据已知条件和棱锥的结构特征，确定面积的最值是关键．
练习册系列答案
相关题目
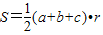，其中a，b，c为三角形的边长，r为三角形内切圆的半径，设S1、S2、S3、S4分别为四面体四个面的面积，r为四面体内切球的半径，利用类比推理可以得到四面体的体积为 ．