题目内容
已知平面内不共线的四点
满足向量
，则
等于（ ）
A． | B． | C． | D． |
C.
解析试题分析：根据向量加减法的三角形法则知
，进而得到两个向量共线即
，再根据共线向量模的关系，即可求解．
考点：向量的共线定理；向量的模．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
，
，求x，y的值使
，且
。平面向量
与
的夹角为60°，
，
，则
( ).
| A．9 | B． | C．3 | D．7 |
，则
的取值范围是（ ）
下列向量中，与向量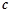
不共线的一个向量
（ ）
A． | B． | C． | D． |
、
，且
=
= 
5
=7.设
为两个非零向量
、
的夹角，已知对任意实数
，
的最小值为1（ ）
A．若确定，则  唯一确定 | B．若确定，则  唯一确定 |
| C．若确定，则 唯一确定 | D．若确定，则 唯一确定 |
，则
的取值范围为（ ）
B．
C
D
若O是
所在平面内的一点，且满足
，则一定是（ ）
| A．等边三角形 |
| B．等腰直角三角形 |
| C．直角三角形 |
| D．斜三角形 |