题目内容
2.已知过点A(1,0)的直线l与曲线C:$\left\{\begin{array}{l}{x=2+2cosα}\\{y=1+2sinα}\end{array}\right.$(α是参数)交于P,Q两点(1)求直线PQ的参数方程
(2)求|AP|+|AQ|的最小值.
分析 (1)由题意求出直线l的参数方程,即是直线PQ的参数方程;
(2)将曲线C的参数方程华为直角坐标方程,将直线l的参数方程代入圆的方程,得到参数t的二次方程,运用韦达定理求出t1+t2、t1t2,再化简|AP|+|AQ|=|t1|+|t2|=|t1-t2|,利用二倍角公式和正弦函数的值域,即可得到最小值.
解答 解:(1)∵过点A(1,0)的直线l的参数方程为:$\left\{\begin{array}{l}{x=1+tcosθ}\\{y=tsinθ}\end{array}\right.$(t为参数),
∴直线PQ的参数方程是:$\left\{\begin{array}{l}{x=1+tcosθ}\\{y=tsinθ}\end{array}\right.$(t为参数),
(2)由曲线C:$\left\{\begin{array}{l}{x=2+2cosα}\\{y=1+2sinα}\end{array}\right.$(α是参数)得,(x-2)2+(y-1)2=4,
∴曲线C的直角坐标方程是(x-2)2+(y-1)2=4,
将直线l的参数方程代入圆的方程,可得t2-2(cosθ+sinθ)t-2=0,
∴t1+t2=2(cosθ+sinθ),t1t2=-2,
则|AP|+|AQ|=|t1|+|t2|=|t1-t2|=$\sqrt{({t}_{1}+{t}_{2})^{2}-4{t}_{1}{t}_{2}}$
=$\sqrt{4(cosθ+sinθ)^{2}+8}$=$\sqrt{12+4sin2θ}$,
∴当sin2θ=-1,即θ=kπ-$\frac{π}{4}$(k∈Z)时,|AP|+|AQ|取得最小值2$\sqrt{2}$.
点评 本题考查参数方程和普通方程的互化,直线参数方程的参数的几何意义及运用,以及韦达定理和正弦函数的值域,考查运算能力,属于中档题.

| A. | (1,-1) | B. | (-1,1) | C. | (0,1) | D. | (0,-1) |
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
| A. | $\left\{\begin{array}{l}{\sqrt{2}x′=\sqrt{5}x}\\{y′=\sqrt{2}y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{\sqrt{2}x′=x}\\{\sqrt{5}y′=\sqrt{2}y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{\sqrt{5}x′=\sqrt{2}x}\\{\sqrt{2}y′=y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{5x′=2x}\\{\sqrt{2}y′=y}\end{array}\right.$ |
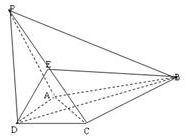 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,且DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2$\sqrt{2}$,PD=2.