题目内容
已知椭圆C的中心在原点,焦点在坐标轴上,短轴的一个端点B(0,4),离心率e=0.6.
(1)求椭圆C的方程;
(2)若O(0,0),P(2,2),试探究在椭圆C内部是否存在整点Q(平面内横、纵坐标都是
整数的点为整点),使得△OPQ的面积S△OPQ=4?若存在,请指出共有几个这样的点(不必具体求出这些点的坐标);否则,说明理由.
(1)  (2)4
(2)4
【解析】
试题分析:(1)设出椭圆的方程,然后利用已知条件列出方程,可求得.
(2) 确定点Q在与直线OP平行且距离为 的直线l上,可得l的方程,再分类讨论,即可求出结论.
的直线l上,可得l的方程,再分类讨论,即可求出结论.
试题解析:【解析】
(1)设椭圆C的方程为 (a>b>0), 1分
(a>b>0), 1分
依题意得,b=4 , ,又a2=b2+c2, 3分
,又a2=b2+c2, 3分
∴a=5 ,b=4 ,c=3, 4分
所以椭圆C的方程为 . 5分
. 5分
(2)依题意得, ,直线OP的方程为 y=x, 6分
,直线OP的方程为 y=x, 6分
因为 ,点Q到直线OP的距离为
,点Q到直线OP的距离为 , 7分
, 7分
所以点Q在与直线OP平行且距离为 的直线l上, 8分
的直线l上, 8分
设l:y=x+m,则 解得m=±4, 10分
解得m=±4, 10分
当m=4时,由 ,消元得41x2+200x<0,即
,消元得41x2+200x<0,即 ,x∈Z,
,x∈Z,
∴x=―4,―3,―2,―1,相应的y也是整数,
此时满足条件的点Q有4个. 14分
考点:直线与圆锥曲线的综合问题
考点分析: 考点1:椭圆的标准方程 考点2:椭圆的几何性质 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 B.
B. C.
C. D.
D.
 ,则输出
,则输出 的值为
的值为
 B.
B. C.
C. D.
D.
 的图像经过点(2,
的图像经过点(2, ),则
),则 = .
= . ,则
,则 =( )
=( ) 在
在 处的切线方程是 .(化成“直线的一般式方程”)
处的切线方程是 .(化成“直线的一般式方程”)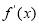 的图象可能是( )
的图象可能是( )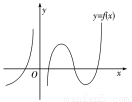
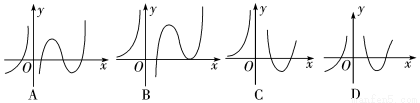

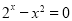 的一个根所在区间为
的一个根所在区间为  为椭圆
为椭圆 的左、右焦点,则在该椭圆上能够满足
的左、右焦点,则在该椭圆上能够满足 的点
的点 共有 个.
共有 个.