题目内容
函数![]() .
.
(Ⅰ)若函数![]() 处的切线与直线
处的切线与直线![]() 平行,且x=1是函数
平行,且x=1是函数![]() 的极值点,求a、b的值;
的极值点,求a、b的值;
(Ⅱ)已知![]() 上是单调递减函数,求
上是单调递减函数,求![]() 的最小值.
的最小值.
解:(Ⅰ)依题意:![]()
当x=-1时,![]() ①
①
当x=1时,![]() ②
②
①②联立 ![]()
解之得 ![]()
(Ⅱ)![]() 上是单调递减函数,
上是单调递减函数,
所在区间[-1,3]上恒有![]()
即![]() 上恒成立
上恒成立
只需满足 ![]()
而![]() 可视为平面区域
可视为平面区域 ![]() 内的点到原点距离的平方.
内的点到原点距离的平方.
其中点(-2,3)距离原点最近,所以 ![]() 有最小值13.
有最小值13.

练习册系列答案
相关题目
 (文)如图所示的程序是计算函数y=f(x)函数值的程序,若输入的x的值为4,则输出的y值为( )
(文)如图所示的程序是计算函数y=f(x)函数值的程序,若输入的x的值为4,则输出的y值为( )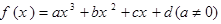 的对称中心为M
的对称中心为M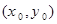 ,记函数
,记函数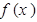 的导函数为
的导函数为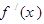 ,
, 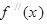 ,则有
,则有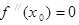 .若函
.若函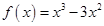 ,则可求得:
,则可求得: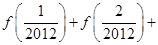
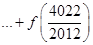
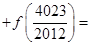 .
.