题目内容
已知 点的坐标是
点的坐标是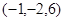 ,
, 点的坐标是
点的坐标是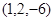 ,
, 为坐标原点,则向量
为坐标原点,则向量 与向量
与向量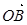 的夹角是( )
的夹角是( )
A. | B.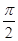 | C.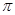 | D.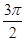 |
C
解析试题分析:因为
 ,
, .
.
考点:空间向量的数量积,及向量的夹角.
点评:由 ,可求得
,可求得 角.
角.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
已知 为坐标原点,
为坐标原点,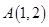 ,点
,点 的坐标
的坐标 满足约束条件
满足约束条件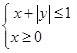 ,则
,则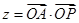 的最大值为
的最大值为
A. | B.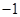 | C.1 | D.2 |
设向量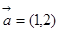 ,
,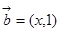 ,当向量
,当向量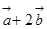 与
与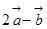 平行时,则
平行时,则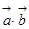 等于
等于
| A.2 | B.1 | C.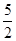 | D.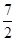 |
已知向量 ,
, ,
, ,则
,则 = ( )
= ( )
A. | B. | C.5 | D.25 |
设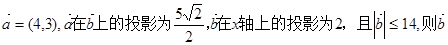 为( )
为( )
| A.(2,14) | B. | C.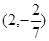 | D.(2,8) |
已知向量 夹角的取值范围是( )
夹角的取值范围是( )
A. | B. | C. | D. |
如图是函数 在一个周期内的图像,M、N分别是最大、最小值点,且
在一个周期内的图像,M、N分别是最大、最小值点,且 ,则A • w的值为( )
,则A • w的值为( )
A. | B. | C. | D. |
设 R,向量
R,向量 且
且 ,则
,则 ( )
( )
A. | B. | C. | D.10 |
已知非零向量a、b满足|a+b|=|a-b|且 的夹角为( )
的夹角为( )
A. | B. | C. | D. |