题目内容
已知函数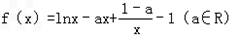 .
.
(I)当a=﹣1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(II)当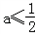 时,讨论f(x)的单调性.
时,讨论f(x)的单调性.
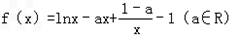 .
.(I)当a=﹣1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(II)当
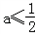 时,讨论f(x)的单调性.
时,讨论f(x)的单调性.解:(I)当a=﹣1时,f(x)=1nx+x+ ﹣1,x∈(0,+∞),
﹣1,x∈(0,+∞),
所以f′(x)= +1﹣
+1﹣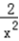 ,
,
因此,f′(2)=1,即曲线y=f(x)在点(2,f(2))处的切线斜率为1,
又f(2)=1n2+2,y=f(x)在点(2,f(2))处的切线方程为y﹣(1n2+2)=x﹣2,
所以曲线,即x﹣y+1n2=0;
(Ⅱ)因为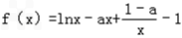 ,
,
所以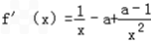 =
=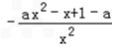 ,x∈(0,+∞),
,x∈(0,+∞),
令g(x)=ax2﹣x+1﹣a,x∈(0,+∞),
(1)当a=0时,g(x)=﹣x+1,x∈(0,+∞),
所以,当x∈(0,1)时,g(x)>0,此时f′(x)<0,函数f(x)单调递增减;
(2)当a≠0时,由g(x)=0,即ax2﹣x+1﹣a=0,解得x1=1,x2= ﹣1.
﹣1.
①当a= 时,x1=x2,g(x)≥0恒成立,
时,x1=x2,g(x)≥0恒成立,
此时f′(x)≤0,函数f(x)在(0,+∞)上单调递减;
②当0<a< 时,
时,  ﹣1>1>0 x∈(0,1)时,g(x)>0,
﹣1>1>0 x∈(0,1)时,g(x)>0,
此时f′(x)<0,函数f(x)单调递减,
x∈(1, ﹣1)时,g(x)>0,此时f′(x)>0,函数f(x)单调递增,
﹣1)时,g(x)>0,此时f′(x)>0,函数f(x)单调递增,
x∈( ﹣1,+∞)时,g(x)>0,此时f′(x)<0,函数f(x)单调递减;
﹣1,+∞)时,g(x)>0,此时f′(x)<0,函数f(x)单调递减;
③当a<0时,由于 ﹣1<0, x∈(0,1)时,g(x)>0,
﹣1<0, x∈(0,1)时,g(x)>0,
此时f′(x)<0函数f(x)单调递减;
x∈(1,∞)时,g(x)<0此时函数f′(x)<0函数f(x)单调递增.
综上所述:当a≤0时,函数f(x)在(0,1)上单调递减;
函数f(x)在(1,+∞)上单调递增
当a= 时,函数f(x)在(0,+∞)上单调递减
时,函数f(x)在(0,+∞)上单调递减
当0<a< 时,函数f(x)在(0,1)上单调递减;
时,函数f(x)在(0,1)上单调递减;
函数f(x)在(1, ﹣1)上单调递增;
﹣1)上单调递增;
函数f(x)在( ﹣1,+∞)上单调递减.
﹣1,+∞)上单调递减.
 ﹣1,x∈(0,+∞),
﹣1,x∈(0,+∞),所以f′(x)=
 +1﹣
+1﹣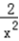 ,
,因此,f′(2)=1,即曲线y=f(x)在点(2,f(2))处的切线斜率为1,
又f(2)=1n2+2,y=f(x)在点(2,f(2))处的切线方程为y﹣(1n2+2)=x﹣2,
所以曲线,即x﹣y+1n2=0;
(Ⅱ)因为
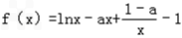 ,
,所以
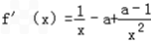 =
=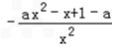 ,x∈(0,+∞),
,x∈(0,+∞),令g(x)=ax2﹣x+1﹣a,x∈(0,+∞),
(1)当a=0时,g(x)=﹣x+1,x∈(0,+∞),
所以,当x∈(0,1)时,g(x)>0,此时f′(x)<0,函数f(x)单调递增减;
(2)当a≠0时,由g(x)=0,即ax2﹣x+1﹣a=0,解得x1=1,x2=
 ﹣1.
﹣1.①当a=
 时,x1=x2,g(x)≥0恒成立,
时,x1=x2,g(x)≥0恒成立,此时f′(x)≤0,函数f(x)在(0,+∞)上单调递减;
②当0<a<
 时,
时,  ﹣1>1>0 x∈(0,1)时,g(x)>0,
﹣1>1>0 x∈(0,1)时,g(x)>0,此时f′(x)<0,函数f(x)单调递减,
x∈(1,
 ﹣1)时,g(x)>0,此时f′(x)>0,函数f(x)单调递增,
﹣1)时,g(x)>0,此时f′(x)>0,函数f(x)单调递增,x∈(
 ﹣1,+∞)时,g(x)>0,此时f′(x)<0,函数f(x)单调递减;
﹣1,+∞)时,g(x)>0,此时f′(x)<0,函数f(x)单调递减;③当a<0时,由于
 ﹣1<0, x∈(0,1)时,g(x)>0,
﹣1<0, x∈(0,1)时,g(x)>0,此时f′(x)<0函数f(x)单调递减;
x∈(1,∞)时,g(x)<0此时函数f′(x)<0函数f(x)单调递增.
综上所述:当a≤0时,函数f(x)在(0,1)上单调递减;
函数f(x)在(1,+∞)上单调递增
当a=
 时,函数f(x)在(0,+∞)上单调递减
时,函数f(x)在(0,+∞)上单调递减当0<a<
 时,函数f(x)在(0,1)上单调递减;
时,函数f(x)在(0,1)上单调递减;函数f(x)在(1,
 ﹣1)上单调递增;
﹣1)上单调递增;函数f(x)在(
 ﹣1,+∞)上单调递减.
﹣1,+∞)上单调递减.
练习册系列答案
相关题目
 .
. ,
, .
. 。
。 的解集;
的解集;