题目内容
已知直线经过椭圆C: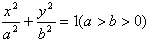 的左顶点A和上顶点D,椭圆C的右顶点为B,点S是椭圆C上位于x轴上方的动点,直线AS,BS与直线
的左顶点A和上顶点D,椭圆C的右顶点为B,点S是椭圆C上位于x轴上方的动点,直线AS,BS与直线 :
: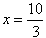 分别交于M,N两点,如图所示。
分别交于M,N两点,如图所示。
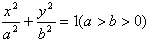 的左顶点A和上顶点D,椭圆C的右顶点为B,点S是椭圆C上位于x轴上方的动点,直线AS,BS与直线
的左顶点A和上顶点D,椭圆C的右顶点为B,点S是椭圆C上位于x轴上方的动点,直线AS,BS与直线 :
: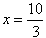 分别交于M,N两点,如图所示。
分别交于M,N两点,如图所示。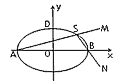
(1)求椭圆C的方程;
(2)求线段MN的长度的最小值;
(3)当线段MN的长度的最小时,在椭圆C上是否存在这样的点T,使得△TSB的面积为 ?若存在,确定点T的个数,若不存在,请说明理由。
?若存在,确定点T的个数,若不存在,请说明理由。
(2)求线段MN的长度的最小值;
(3)当线段MN的长度的最小时,在椭圆C上是否存在这样的点T,使得△TSB的面积为
 ?若存在,确定点T的个数,若不存在,请说明理由。
?若存在,确定点T的个数,若不存在,请说明理由。 解:(1)由题意,得椭圆方程为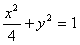 。
。
(2)设直线AS的方程为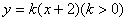 ,
,
从而可知M点的坐标为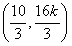 ,
,
由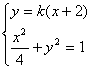 ,得
,得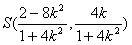 ,
,
所以可得BS的方程为 ,
,
从而可知N点的坐标为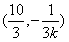 ,
,
∴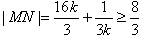 ,当且仅当
,当且仅当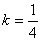 时,等号成立,
时,等号成立,
故当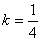 时,线段MN的长度取最小值
时,线段MN的长度取最小值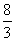 。
。
(3)由(2)知,当|MN|取最小值时,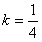 ,
,
此时直线BS的方程为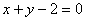 ,
,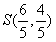 ,
,
∴|BS|=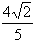 ,
,
要使椭圆C上存在点T,使得△TSB的面积等于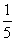 ,只需T到直线BS的距离等于
,只需T到直线BS的距离等于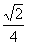 ,
,
所以点T在平行于直线BS且与直线BS的距离等于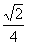 的直线
的直线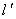 上。
上。
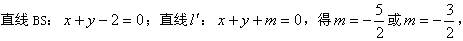
则直线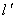 :
: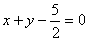 或
或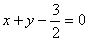 ,
,
联立,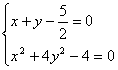 ,△<0,无解;
,△<0,无解;
 ,△=44>0,有两个解;
,△=44>0,有两个解;
所以T有两个。
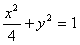 。
。(2)设直线AS的方程为
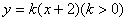 ,
,从而可知M点的坐标为
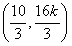 ,
,由
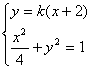 ,得
,得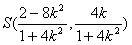 ,
,所以可得BS的方程为
 ,
,从而可知N点的坐标为
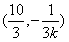 ,
,∴
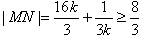 ,当且仅当
,当且仅当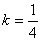 时,等号成立,
时,等号成立,故当
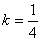 时,线段MN的长度取最小值
时,线段MN的长度取最小值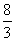 。
。(3)由(2)知,当|MN|取最小值时,
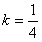 ,
,此时直线BS的方程为
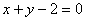 ,
,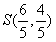 ,
,∴|BS|=
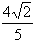 ,
,要使椭圆C上存在点T,使得△TSB的面积等于
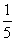 ,只需T到直线BS的距离等于
,只需T到直线BS的距离等于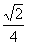 ,
,所以点T在平行于直线BS且与直线BS的距离等于
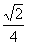 的直线
的直线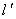 上。
上。 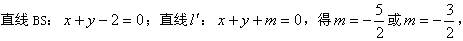
则直线
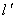 :
: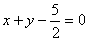 或
或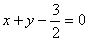 ,
,联立,
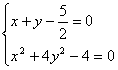 ,△<0,无解;
,△<0,无解; ,△=44>0,有两个解;
,△=44>0,有两个解;所以T有两个。

练习册系列答案
相关题目
 经过椭圆S:
经过椭圆S: 的一个焦点和一个顶点.
的一个焦点和一个顶点. 轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k.
轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k.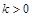 ,求证:
,求证: .
.